How to Measure Sinusoids and Noise Spectrally using Gnu Radio (Corrected)

Gary Schafer, 3 January 2026 (updated 9 January 2026)

UPDATE: 10 January 2026: The whole point of this post and the previous one was to deal with noise and power spectral measurements. Should have just looked online first. Neil Robertson has several posts over at DSP Related.com, including a general method for calculating spectral power, using the "pwelch" function to calculate power spectral density (PSD) (as well as another, more general method), calculating the power of a sinusoid in a spectrum, and his latest (done less than a week ago!) covering spectrum averaging. Having read through his posts, I've realized that you can accurately measure both coherent and noncoherent at the same time. It's based on how you measure the power levels (single point at the center vs the whole curve). I've reworked this post to better explain that.

Happy New Year to you all! I'm going to finish up a few loose ends with respect to my last post discussing issues measuring SNR using a spectral display. For this post, I'm going to explain some of the complexity of measuring sinusoids and noise using the Gnu Radio QT GUI Frequency Sink.

In my original post, I looked at measuring signals based on whether they were coherent (a sinusoid or similar) vs noncoherent (aka noise). Now I'm just going to look at how you measure the signal whether it is as a single point (the peak measurement) or all of the points that make up that signal (band measure).

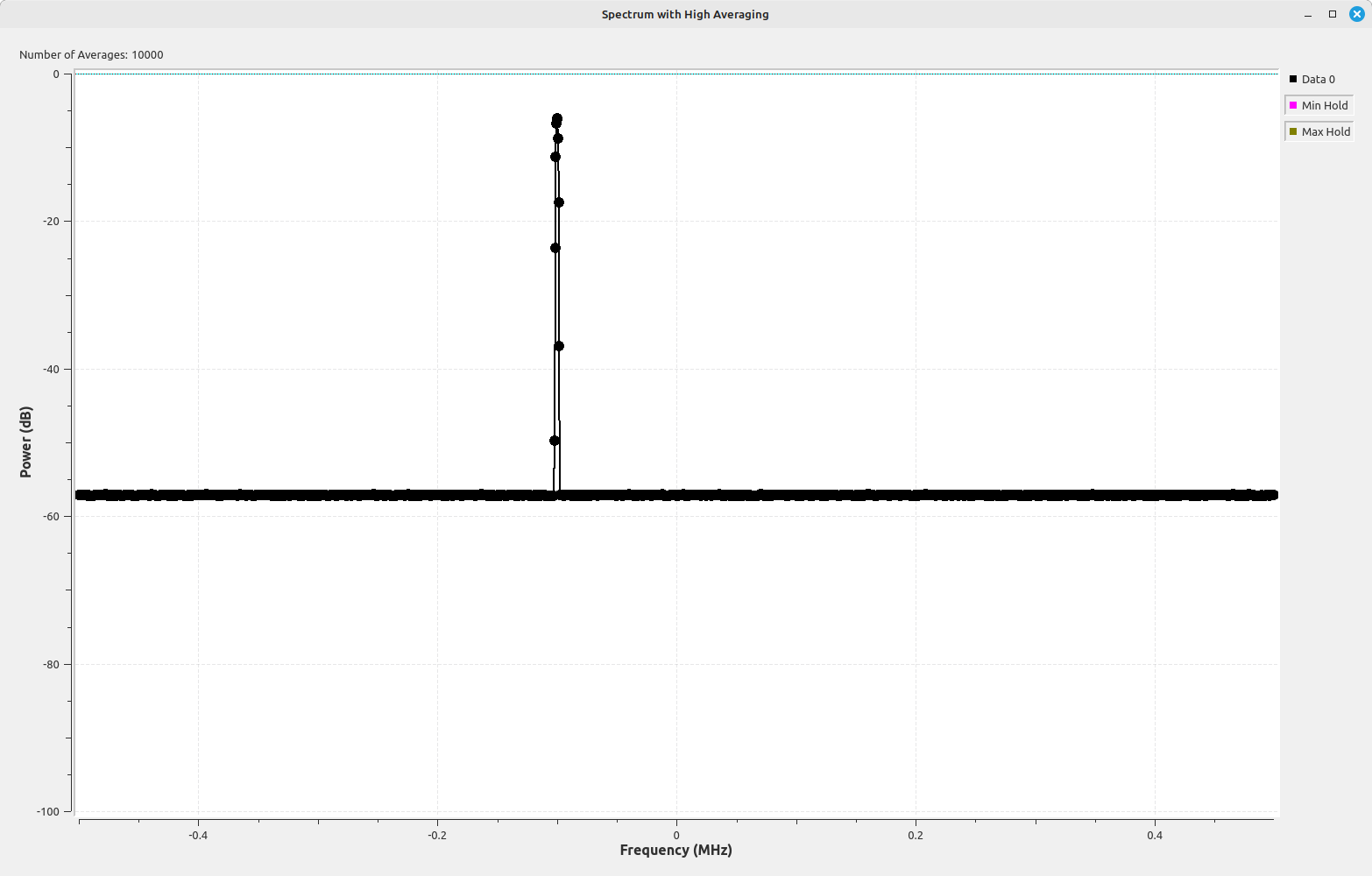
2D graph showing a horizontal line running from left to right roughly middle of the graph. A vertical line extends from the horizontal line roughly left of center, and extends up almost to the top of the graph. — Spectrum of a sinusoid and noise floor using a moving average with a value of 10000.

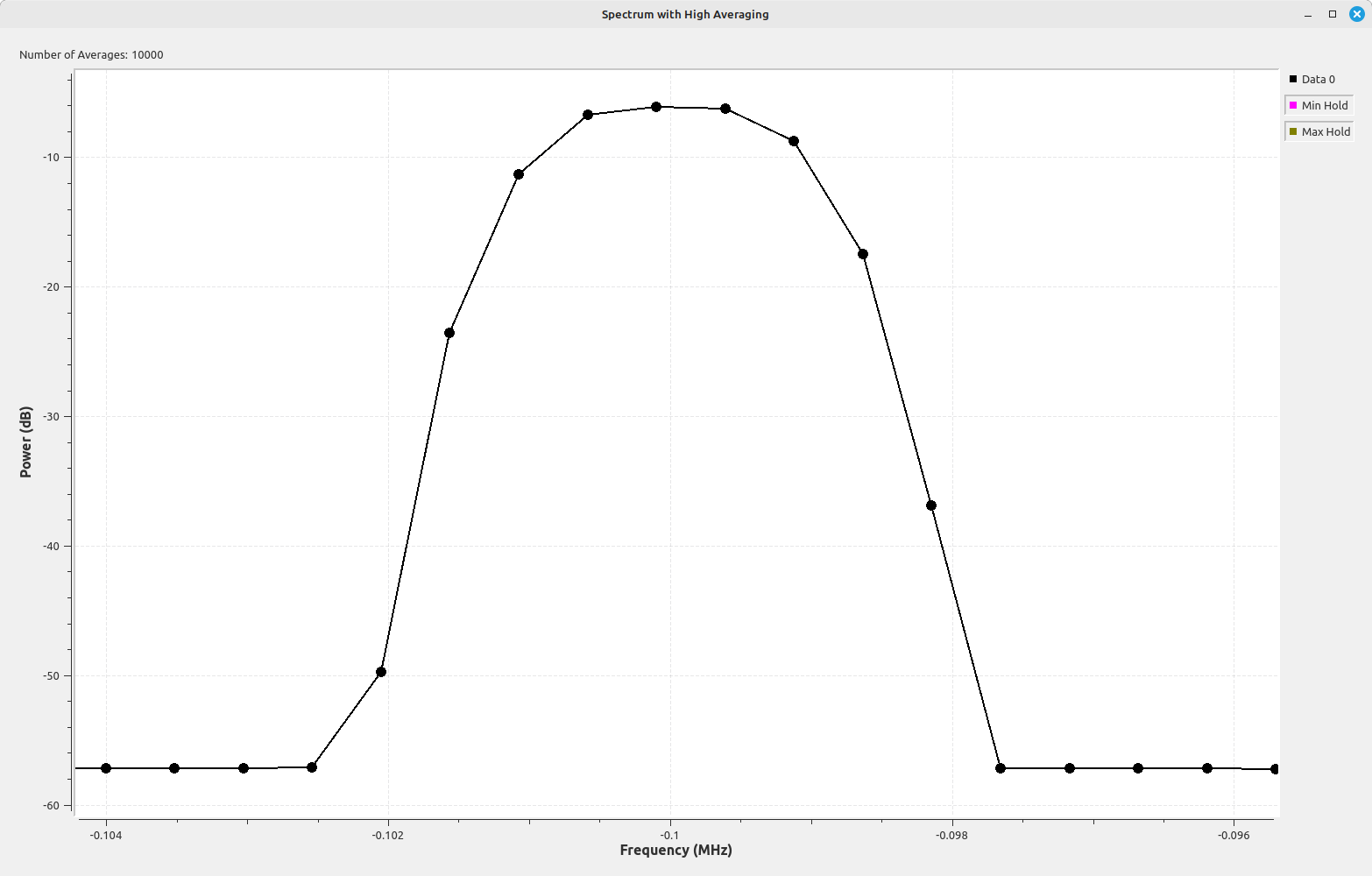
2D graph showing a line near the bottom of the graph and a rounded line rising from the bottom and extending almost all the way to the top, before going back down to the bottom. — Zoomed in view of a sinusoid on a spectral display. In this case, the data has been windowed with a flattop window. Flattop windows are a class of windows that provide accurate peak values, but it also spreads out the energy over many bins.

I'm going to boil down the problem of measuring power spectrally. It's spectral leakage. The typical "solution" for spectral leakage is windowing. To quote fred harris' paper[1]:

Windows are weighting functions applied to data to reduce the spectral leakage associated with finite observation intervals.

Spectral leakage and windowing create two problems with accurate spectral measurements. These are:

Scalloping loss: This occurs due to the aforementioned spectral leakage, a problem that only occurs in DFT / FFT displays. You won't find this in analog spectrum analyzers.
Window processing gain: Windows might alleviate some (or almost all) scalloping loss, but they also reduce the signal energy at the same time.

Graph showing two overlaid sinusoids, one in blue and one in red. The individual cycles are so close in time that they are difficult to discern. — A time record of a complex sinusoid. This particular time record shows 8192 samples.

Graph of two overlaid sinusoids, one in blue and one in red. The cycles of the sinusoid are so close together that it is difficult to see the individual cycles. The sinudoids are a zero amplitude at each end, and grow in amplitude as the signal gets to the center of the graph. — Windowed time record of a complex sinusoid. Note how the sinusoid has zero amplitude at each end, and rises towards the center. These values at each end lead to a lower overall power level. This is called the "processing gain" (once again, actually a loss) of the window.

Windows have a slew of different parameters, which harris also covered in his 1978 paper. But two of the most important for measuring power spectrally are the incoherent power gain and the coherent power gain. The values can be calculated as follows:

Incoherent power gain = sum(w²)/N

Coherent power gain = (sum(w)/N)²

Think of these two values as "correction factors" that can be applied to the measured spectral power levels. But they're different values. So which one do you apply? You apply the one that you need depending on how you're going to measure the signal levels.

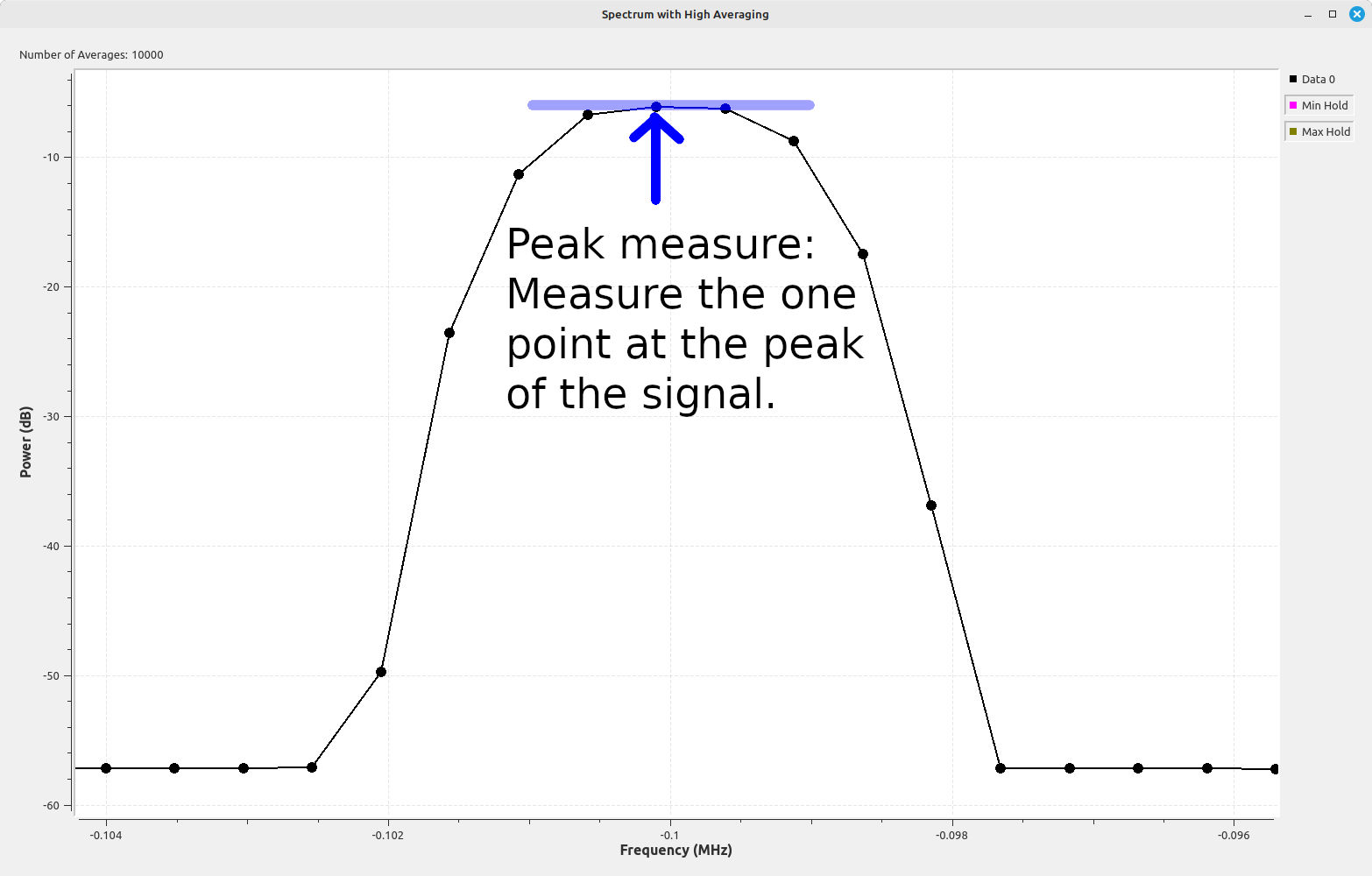
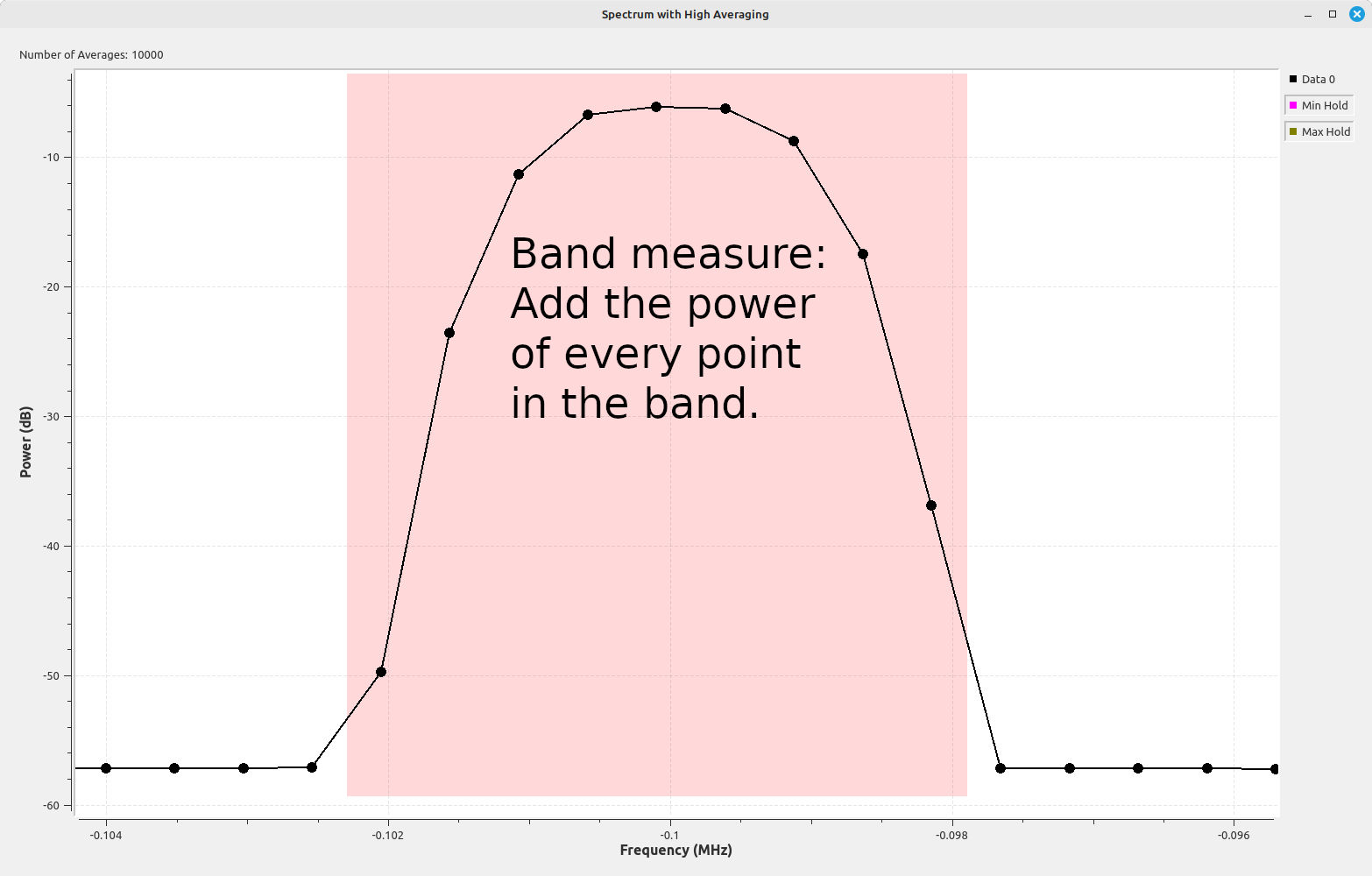
If you're going to measure the peak of the signal (say using a single marker that the spectral display may provide), then you'll want to use the coherent power gain. If you're going to measure the band power of the signal, meaning all of the points in the spectrum that make up that signal, then you'll want to use the incoherent power gain.

There's another value that's important with respect to these measurements. This is the normalized equivalent noise bandwidth or NENBW. This is the "window factor" that is used to calculate the resolution bandwidth (RBW) of the spectral display when using a specific window. The NENBW is typically expressed as a linear value, and is equal to the incoherent power gain divided by the coherent power gain. For example, the Blackman-harris window used in the QT GUI Frequency Sink has an incoherent power gain of -5.884 dB, and a coherent power gain of -8.91 dB. Since they are in decibels, we can "divide" by subtracting these two values, which gives us -5.884 - (-8.91) = 3.026 dB. In linear, this is 10^(3.026/10) = 2.007, which is pretty close to the more-precise value of 2.0044 (given the issues of rounding dB values).

What we'll discover as we go along is that we can convert from one measurement to another using these different "correction" factors.

The incoherent power gain, the coherent power gain, the scalloping loss, and the NENBW of a window can be calculated. The values for most of the windows used in Gnu Radio are tabulated below.

Window	Incoherent Power Gain (dB)	Coherent Power Gain (dB)	Scalloping Loss (dB)	NENBW (bins)
Uniform (aka Rectangular)	0	0	3.92	1.0000
Hanning	-4.260	-6.02	1.42	1.5000
Hamming	-4.008	-5.35	1.75	1.3628
Blackman (approx)	-5.1627	-7.54	1.10	1.7268
4-Term Minimum Blackman-harris	-5.884	-8.91	0.83	2.0044
Nuttall4b	-5.9205	-8.98	0.81	2.01212
Stanford Research Flattop ("Flat-top" in Gnu Radio)	-7.5593	-13.32	0.0156	3.7702

Measuring Peak Power

Historically, systems were geared towards using peak measurements. For example, this FCC test report on a Kyocera cellphone from the early 2000s measured its output power using an analog-based spectrum analyzer. The analyzer's RBW has been set to be equal to the bandwidth of the cellphone's transmission (the curved line at the top of the display). This ensures it captures all of the energy of the signal. The user set the reference level (top line of the display) at the peak to measure its total power. Hence, this is a peak measurement.

2D graph showing a 10 x 10 grid of squares. A line starts in the lower, lefthand corner, rises towards the center where it jumps up in five peaks, then lowers back down to the lower, righthand corner. A smooth curve starts on the left side roughly half-way up, curves up to the center where it touches the top of the grid, then curves back down where it ends on the right side, also roughly half-way between top and bottom. Various annotations are written in the grid, and other generated annotations are placed around the bottom, left side and top of the grid. — Spectral display from a Kyocera FCC test report on one of its cellphones license applications. This display shows the output of a test cellphone within the frequency range of the US 800 MHz cellular band. The display shows both a narrow RBW display as well as an earlier capture using a large RBW (the curved line at the top of the display. The user has set the reference level (the top line of the display) to be equal to that of the large RBW curve, allowing for measurement of the output power. This is an example of *peak measurement*, as the measured level at the peak of the large RBW curve is also the measured output power of the cellphone. (Image credit: Kyocera Wireless Corporation, FCC ID OVFKWC-2135, 2001)

Digital systems are different. Since each point on a digital spectral display is just a number, its possible to display the data however you want, then say, "How much power is in these points combined?" For a computer, this is the proverbial "childs play". This is a "band measure", not "peak measure". The problem is that, if you're not careful, measuring band power on a display that is corrected for peak power will give you incorrect readings.

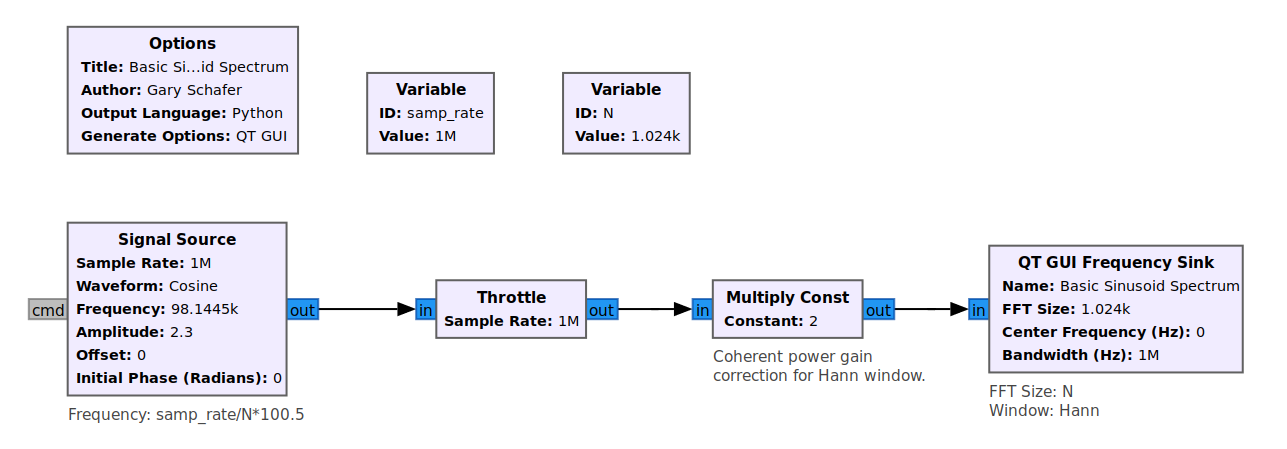
Let's start by measuring the power of a sinusoid. For this, I'll create a very basic flowgraph in Gnu Radio Companion (GRC). Below is the flowgraph and the initial display.

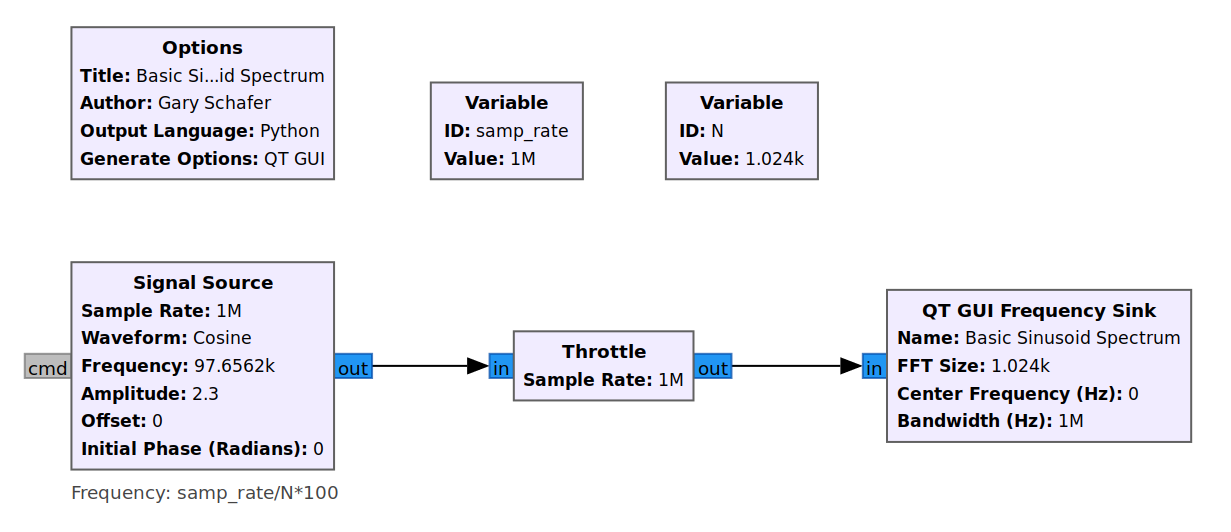
Block diagram showing two horizontal rows of squares. Each row contains three squares. The top row shows the squares unconnected, whereas the bottom row shows the squares connected by lines going from left to right. — Gnu Radio Companion flowgraph for looking at the spectrum of a sinusoid. The sinusoid frequency has been set such that it will be centered on a frequency bin of the FFT. That's the "samp_rate/N*100" in the "Signal Source" frequency. The frequency display is using a "rectangular" window.

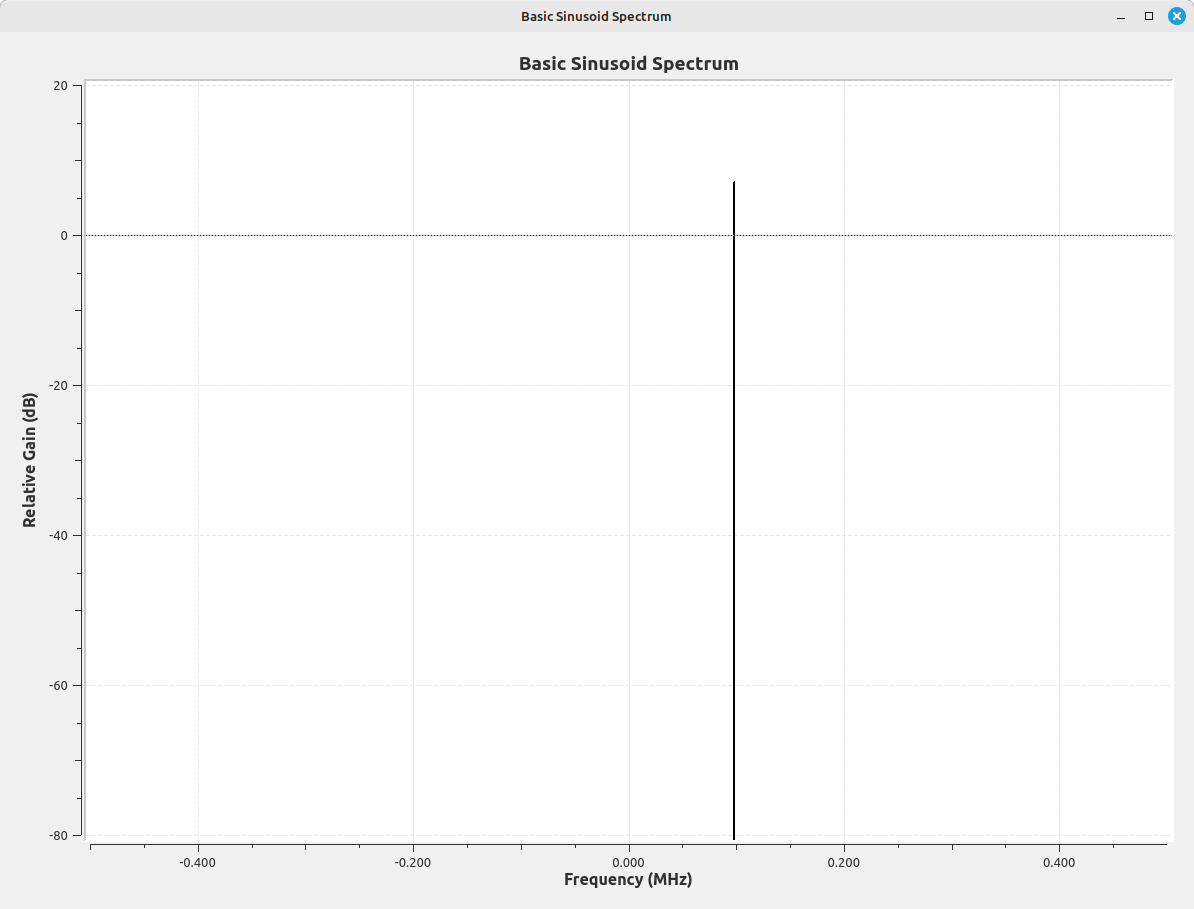
2D graph showing a vertical line extending from the bottom almost all of the way to the top of the display. The line is just right of center. — Display of the sinusoid with the frequency set such that it is centered within a frequency bin.

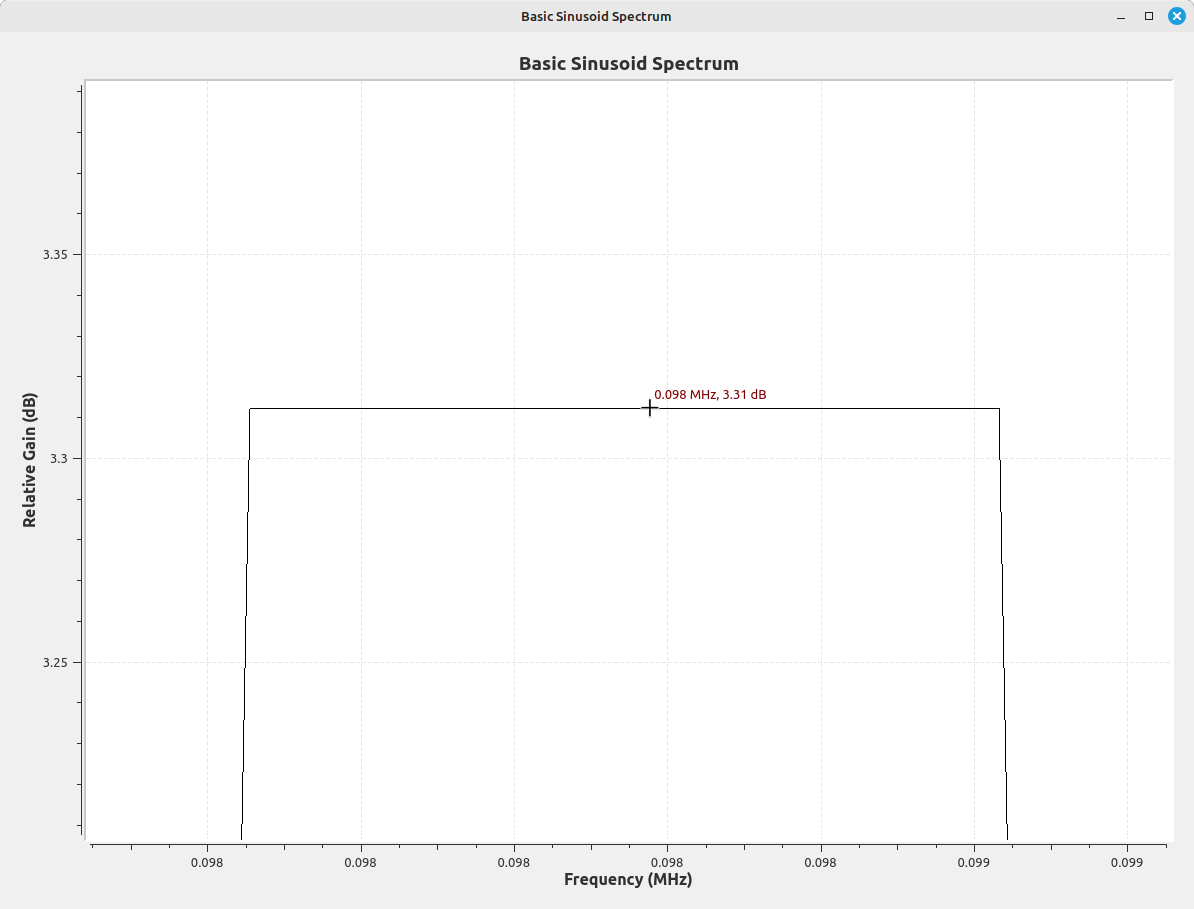
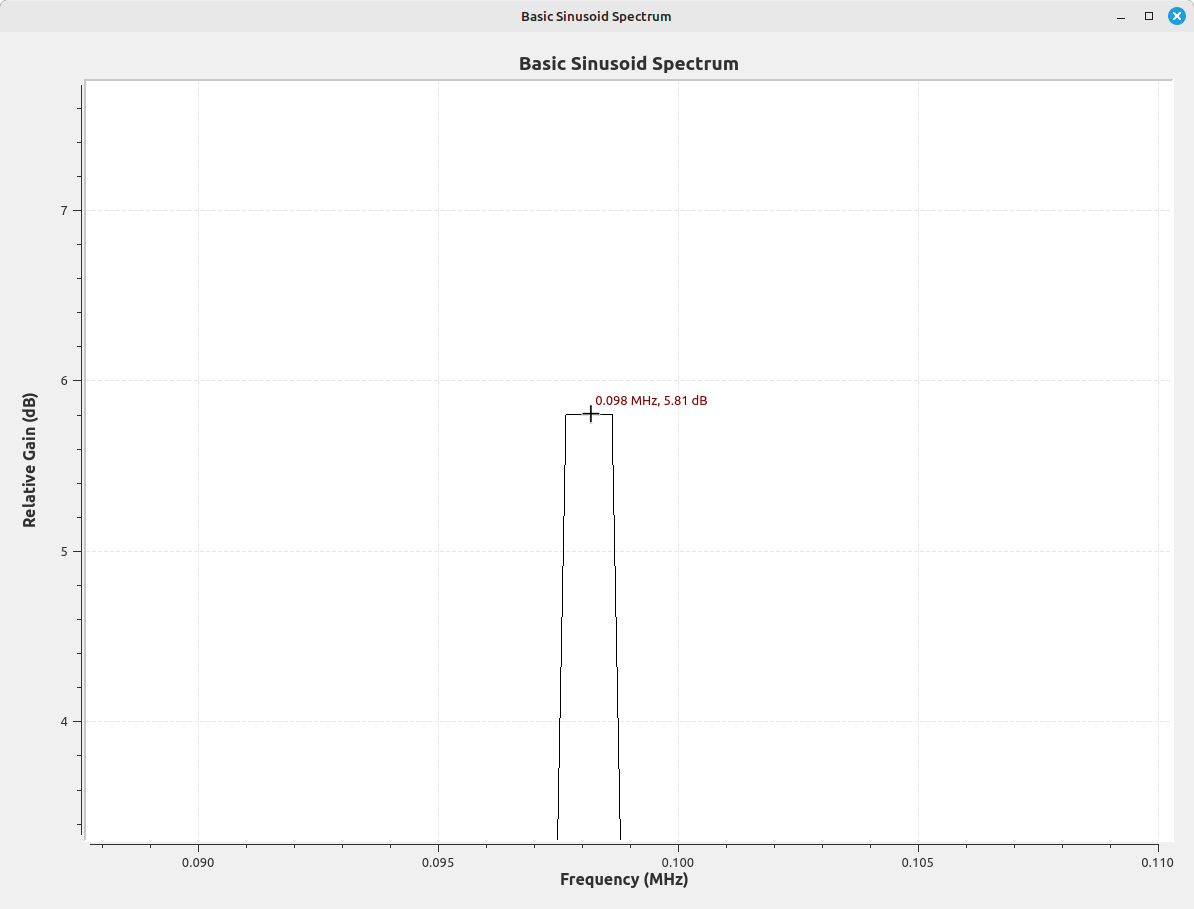
Again, the frequency display is set to be "unwindowed" (uses a "rectangular" window). If we zoom in on the peak of the displayed signal, it measures at 7.23 dB. This corresponds to the power of the sinusoid, which is set to a magnitude of 2.3. The linear power of the signal (assuming its going into a unity or 1 Ω load) is 2.3² = 5.29. Converting this to dB, we get 10*log₁₀(5.29) = 7.23.

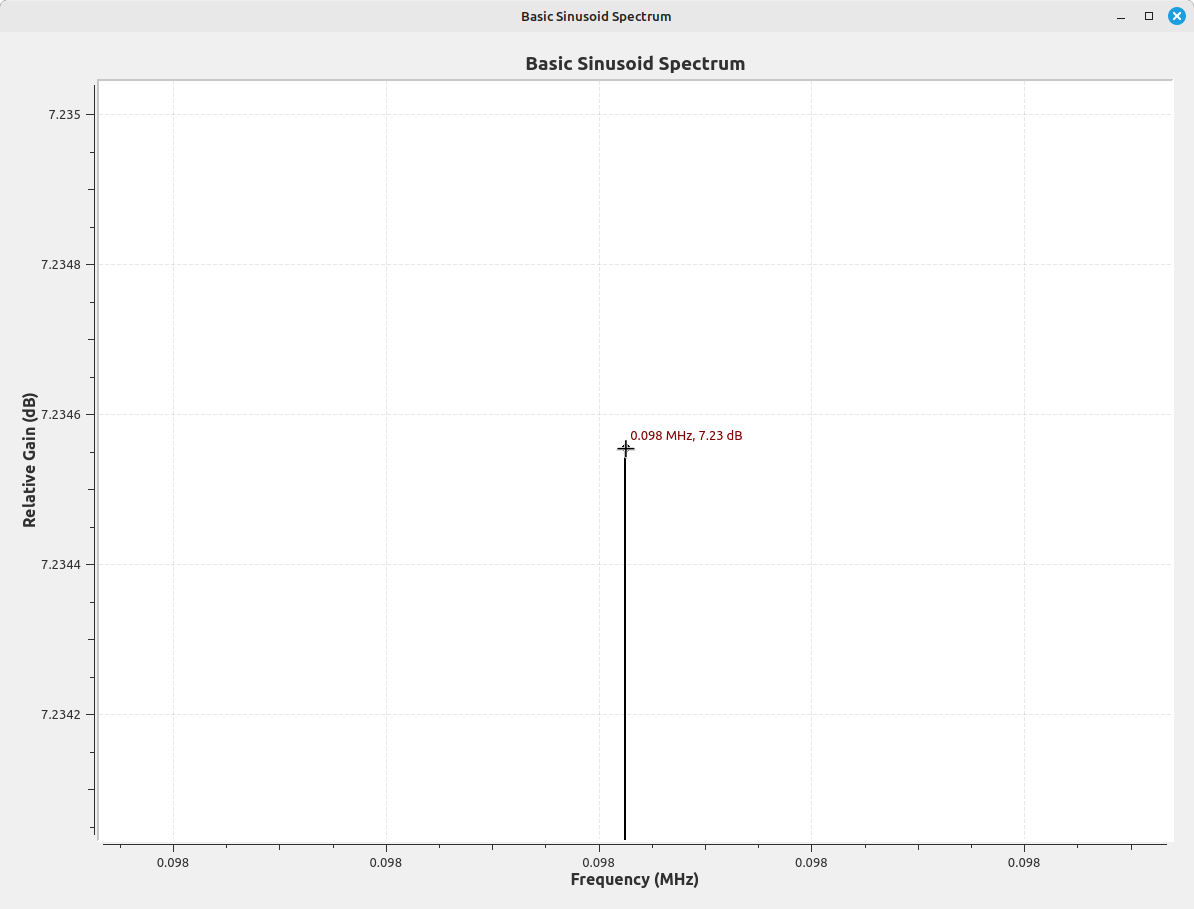
2D graph showing a vertical line that extends from the bottom of the graph up roughly halfway. The line is centered horizontally. At the top of the line is a plus sign with text next to it. — This graph shows the marker being used to measure the power of the sinusoid. It measures perfectly at 7.23 dB, just as calculated.

Now, what happens if we adjust the sinusoid frequency such that it is as the edge of a frequency bin instead of at the center? We get a mess is what we get.

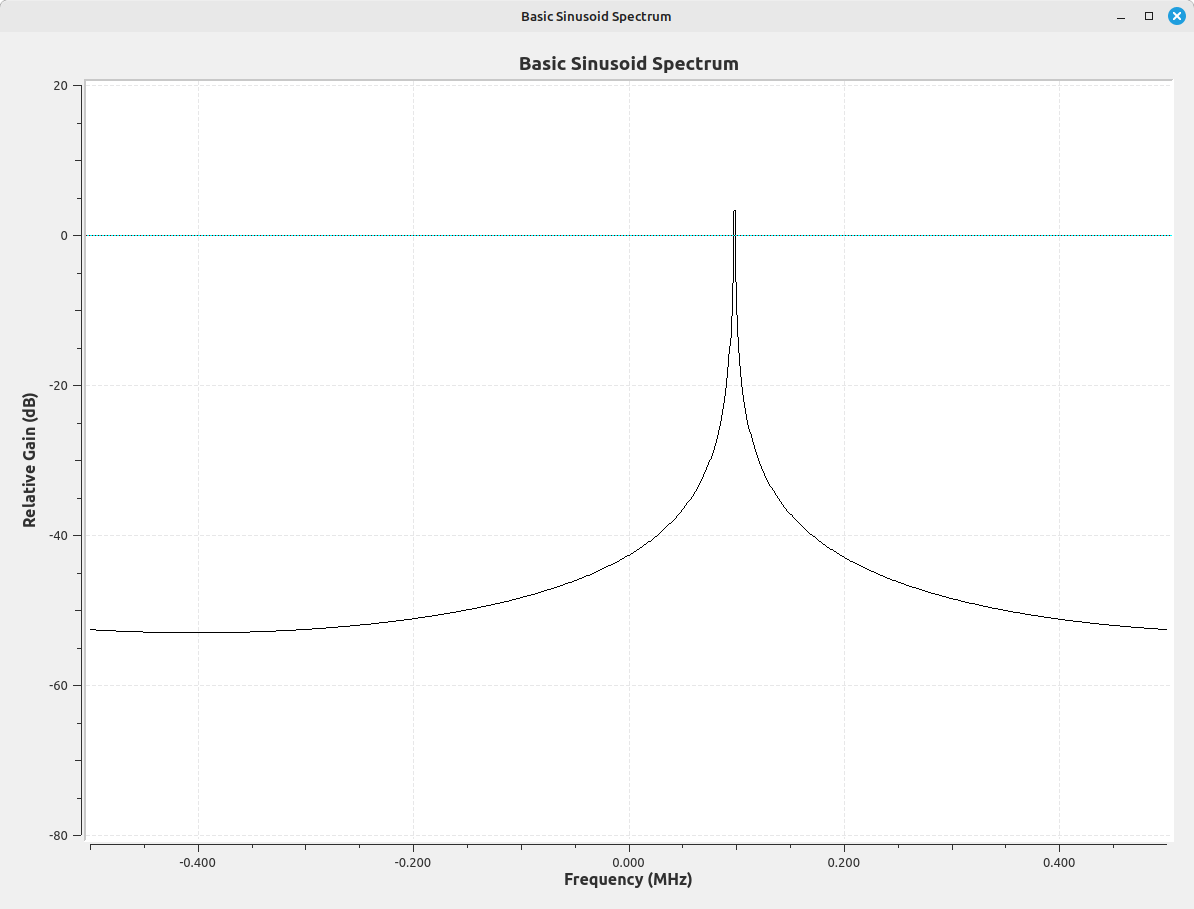
2D graph showing a peak near the top center of the graph, and falling away on either side in a curve. — Spectrum of a sinusoid that is not centered in a frequency bin. The single line (when centered in a bin) has now turned into... this mess. The energy of the sinusoid has now been smeared allllllll over the spectrum. This is *spectral leakage*.

2D graph showing a thin, horizontal line roughly halfway between top and bottom and with a length of 1/5 of the width. Lines from each end of the graph towards the bottom of the graph. — Zoomed in view of the peak of the sinusoid that is at the edge of a frequency bin. The peak is set to 3.31 dB. The original power level was measured at 7.23 dB. This is *scalloping loss*. An unwindowed display will have a maximum scalloping loss of 3.92 dB. If we started with 7.23 - 3.92 = 3.31 dB. The rest of the power is now smeared over the rest of the spectrum.

With unwindowed signals, we wind up with a lot of scalloping loss (energy spread over the spectrum due to signals not being centered in frequency bins). Scalloping loss is uncorrectable. Hence, the introduction of windowing, the application of a weighted time series to reduce scalloping loss and spectral leakage.

Let's start with a basic Hann window. (NOTE: It's actually not a very good window, but it's easy to create and will demonstrate the important points.) We can create this window with the following equation:

w = 0.5 - 0.5*cos(2*π*n/N)

where:

w = window values
n = 0,1,2...N-1
N = number of points in the time record

From these windows values, we can calculate the following parameters:

Coherent power gain: This corresponds to the drop of the peak power of the signal. It can be calculated as (sum(w(n)/N)². For a Hann window, this is 0.25 = -6.02 dB.
Incoherent power gain: This corresponds to the drop of every frequency point of the signal. It can be calculated as sum(w²(n))/N. For a Hann window, this is 0.375 = -4.26 dB.
Normalized Equivalent Noise Bandwidth (NENBW): This is the incoherent power gain divided by the coherent power gain. For the Hann window, this is 0.375 / 0.25 = 1.5 bins.
Processing gain: This is sum(w)/N. This is 0.5 = -3.01 dB for the Hann window. This is the square root of the coherent power gain.

If we use a Hann window on our sinusoid, we get the following graph.

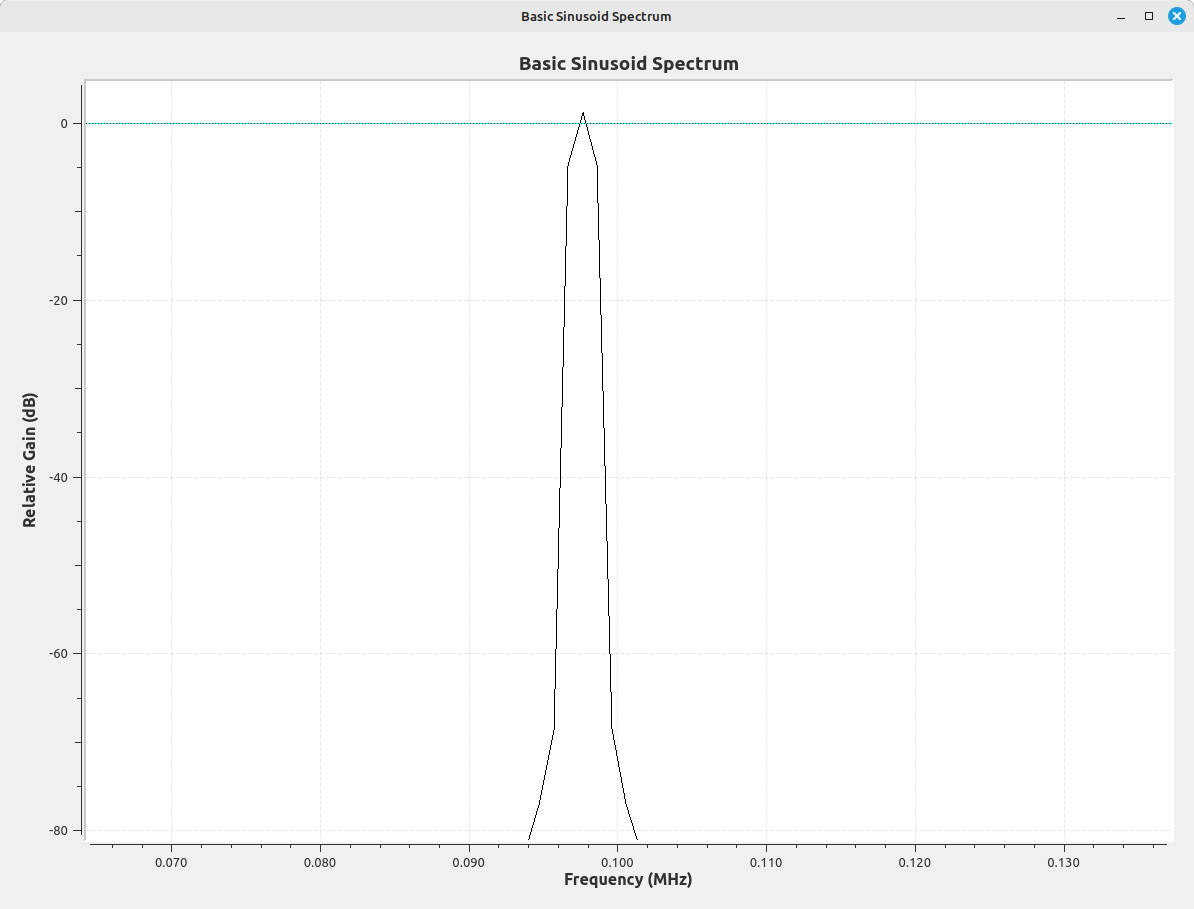
2D graph showing two closely-spaced, thin lines extending from the bottom of the graph towards the top. The lines meet at a thin point. — Spectrum of a Hann-windowed sinusoid. Note that, compared to the unwindowed sinusoid, this spectral display of a sinusoid has a slight width to it.

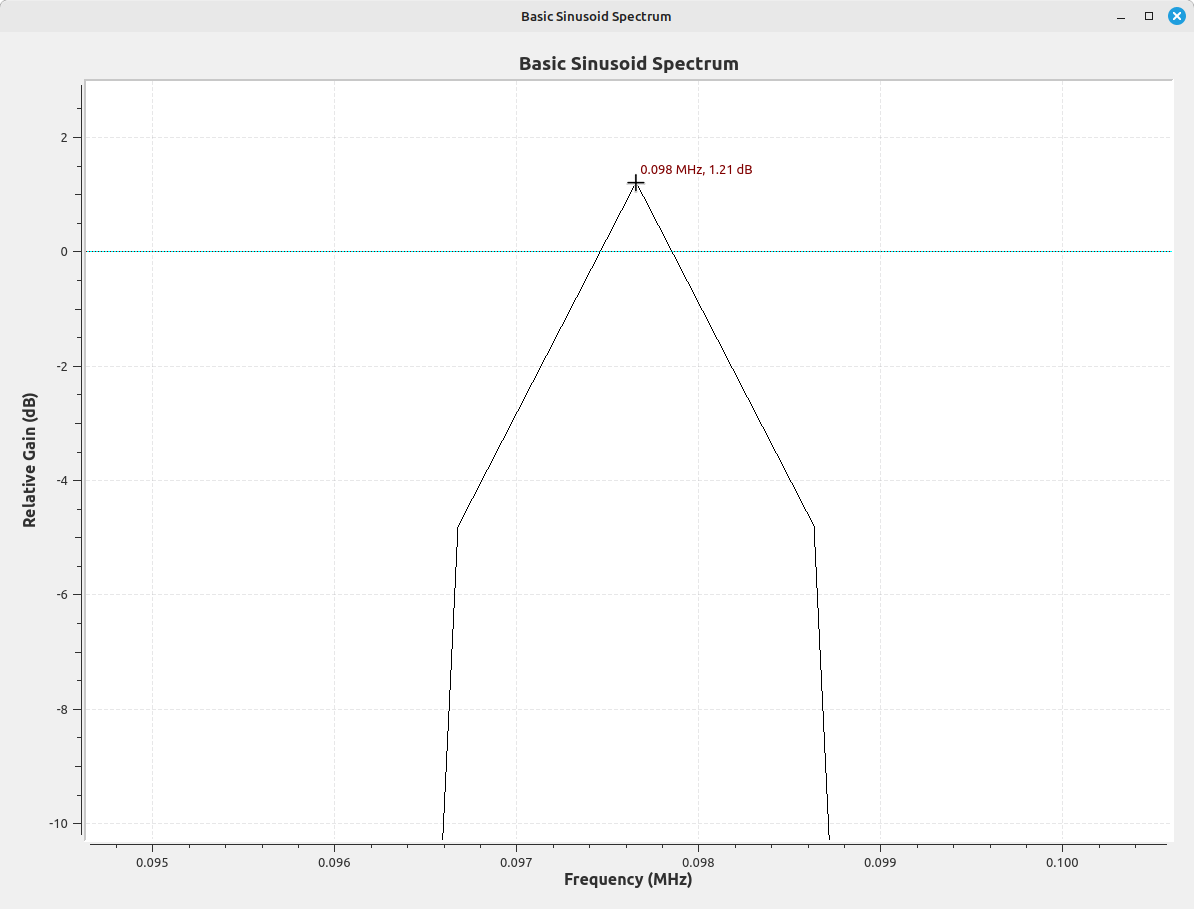
2D graph showing two closely-spaced, thin lines extending from the bottom of the graph towards the top. The lines meet at a thin point. A small plus sign rests at the top of the point with some text next to it. — Zoomed-in view of the Hann-windowed sinusoid showing the peak of the signal. The unwindowed level was 7.23 dB. The coherent power gain is -6.02 dB, which leads to this measured level of 7.23 - 6.02 = 1.21 dB.

If we also use it on the non-centered sinusoid, we get the following:

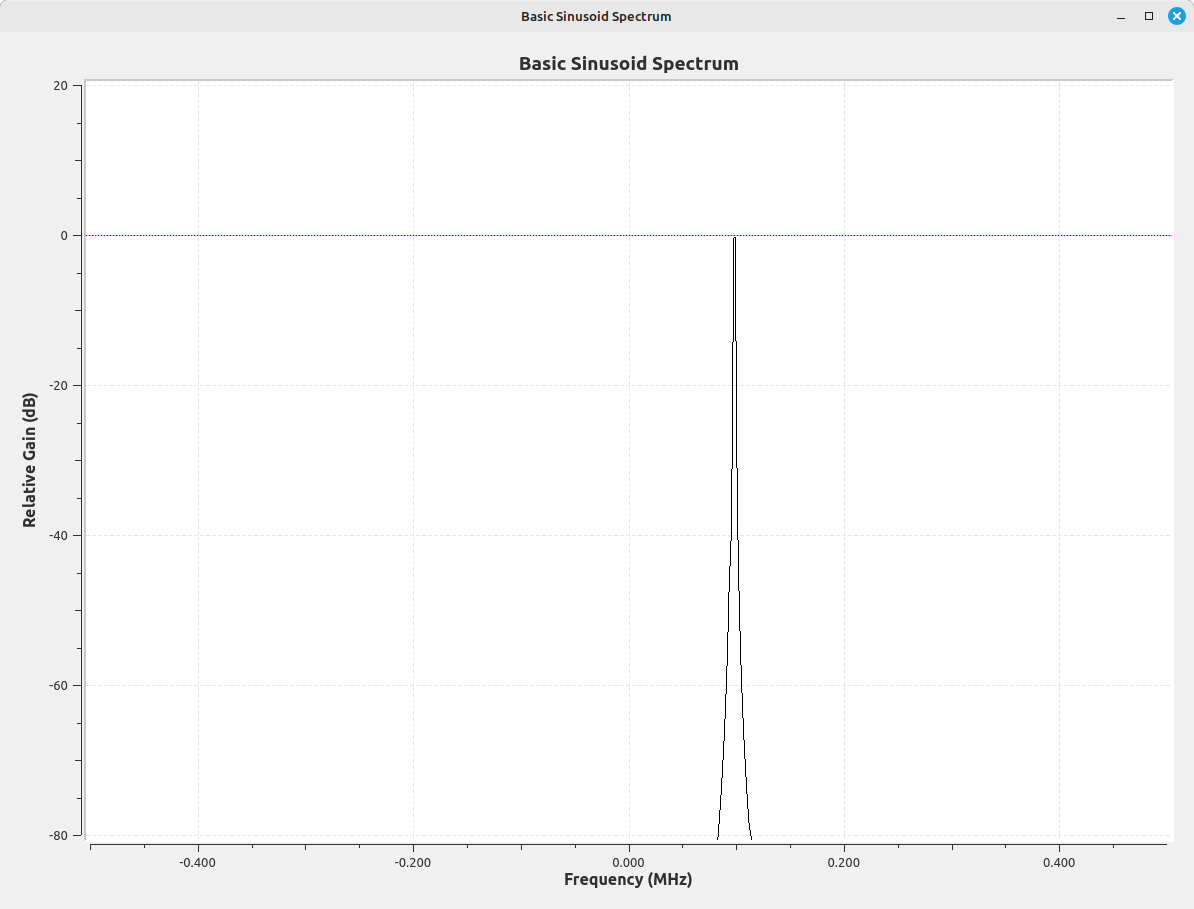
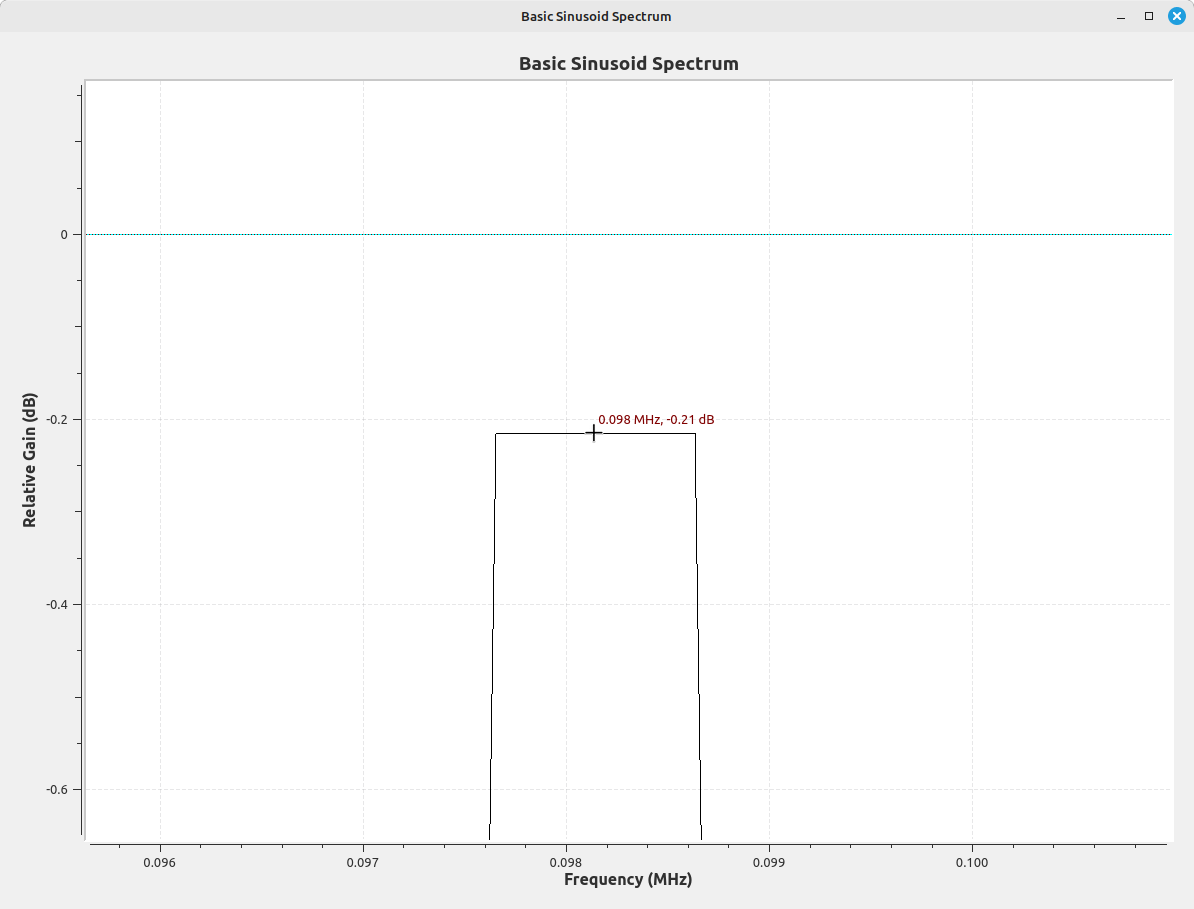
If we correct for the peak power, we can increase the amplitude of each point by 6.02 dB (multiply time domain samples by 2 to increase power by 4). This gives us the corrected spectrum, but there's still scalloping loss.

Block diagram of squares in two horizontal rows. The top row consists of three, unconnected squares. The bottom row consists of four squares connected by lines from left to right. — Modified flowgraph to correct for the coherent power loss. The Hann window has a loss of 6.02 dB (linear factor of 4). This corresponds to a magnitude value of 2.

Thin vertical rectangle extending from the bottom of the graph up to roughly halfway to the top. At the top is a plus sign with text next to it. — Zoomed-in view of the corrected sinusoid centered at a bin edge. The actual value is 7.23, but is measured here at 7.23 - 1.42 = 5.81 dB. The difference is due to the (uncorrectable) scalloping loss.

Correcting for Scalloping Loss

Even with the coherent power gain correction, the actual amplitude of an unwindowed, unmodulated tone can still be off by just less than 4 dB. Again, this offset is due to scalloping loss. There are a few, different ways to deal with scalloping loss. I'll look at two methods.

Zeropadding

The first method involves zeropadding the time domain signal. The original signal is collected into a time record, windowed, then zeros are added to the end of the time record before it is fed into the FFT routine. This has the affect of interpolating in the frequency domain. To demonstrate this in Gnu Radio, I can't use the "QT GUI Frequency Sink" as it provides no method to zeropad the time record. I've created a new flowgraph that implements a frequency display, but with the ability to zeropad the time record.

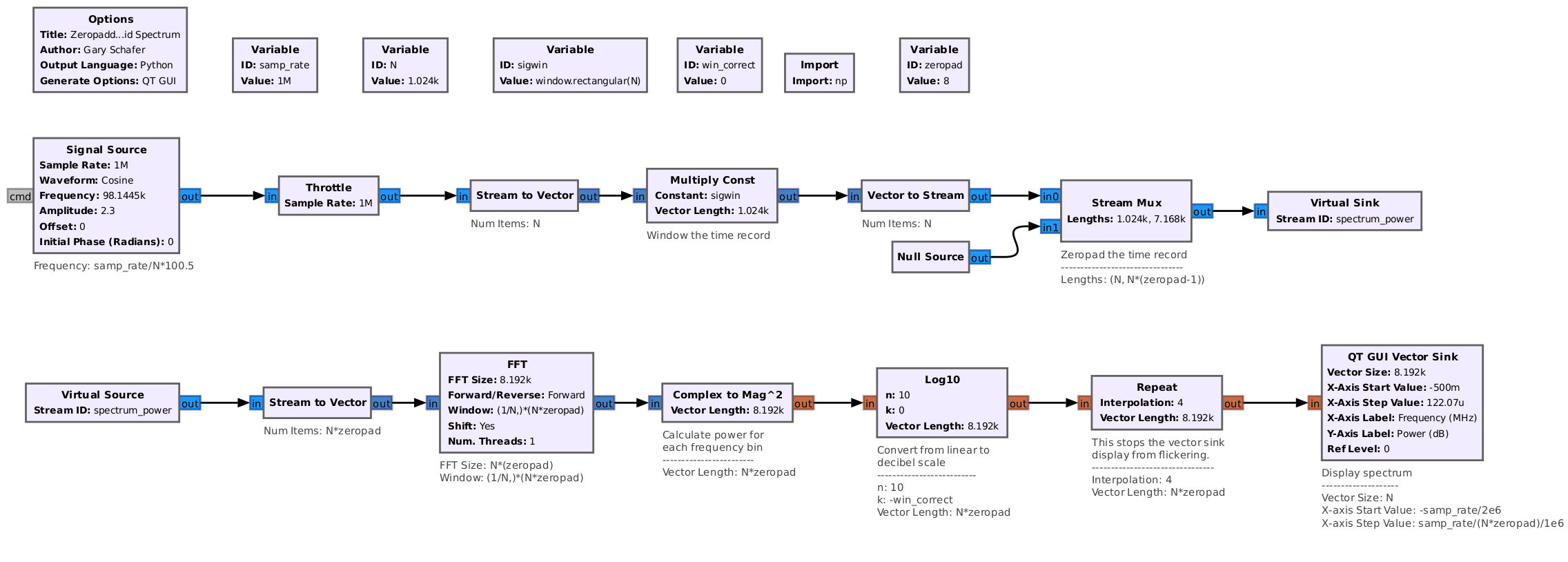
Block diagram showing three, horizontal rows of squares. The top row consists of seven squares unconnected to anything. The second and third rows consist of severn squares each that are connected with thin lines running from left to right. — GRC flowgraph that takes an input signal, windows it, zeropads it, then calculates and displays the spectrum.

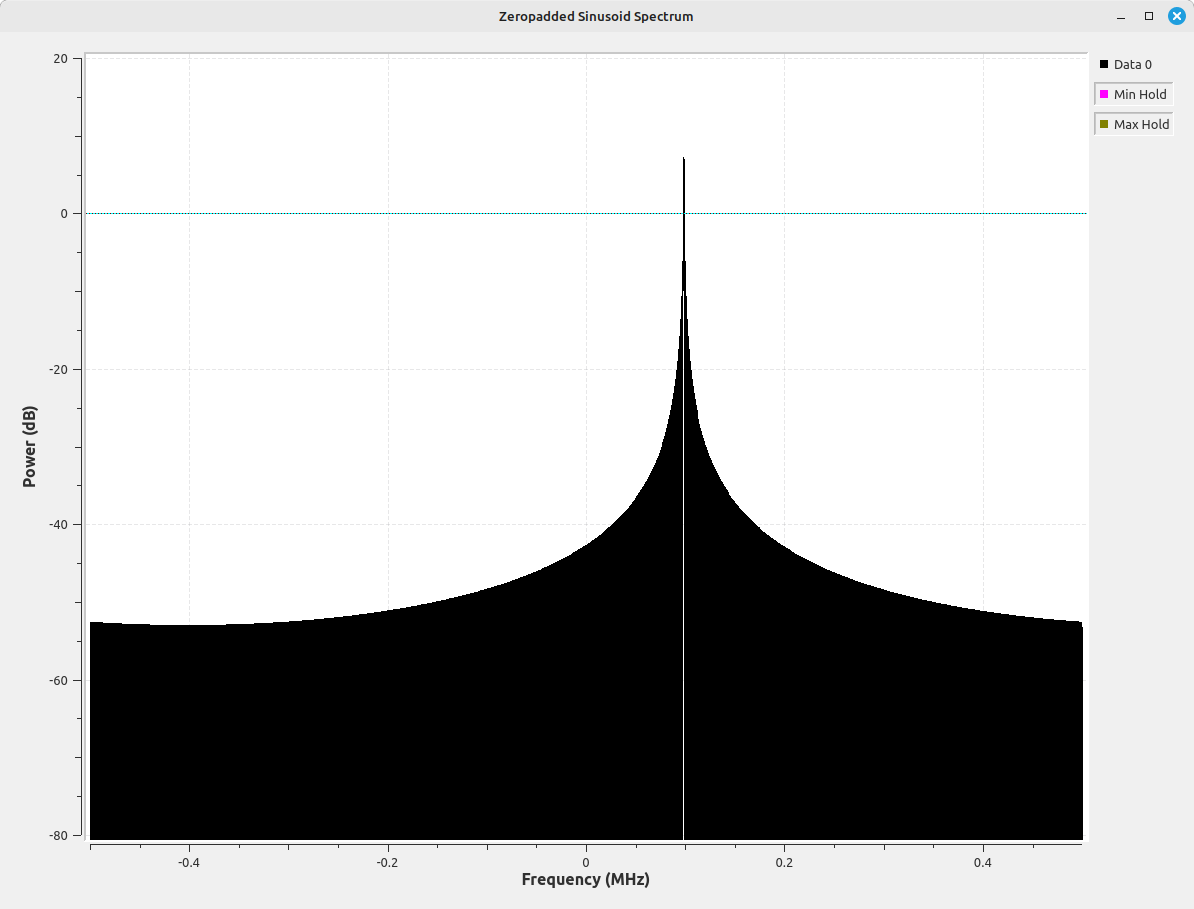
2D graph showing a peak near the top center of the graph, and falling away on either side in a curve. The area under the curve is black, while the area above the curve is white. — Display of zeropadded sinusoid in which the center frequency of the sinusoid is at the edge of a frequency bin.

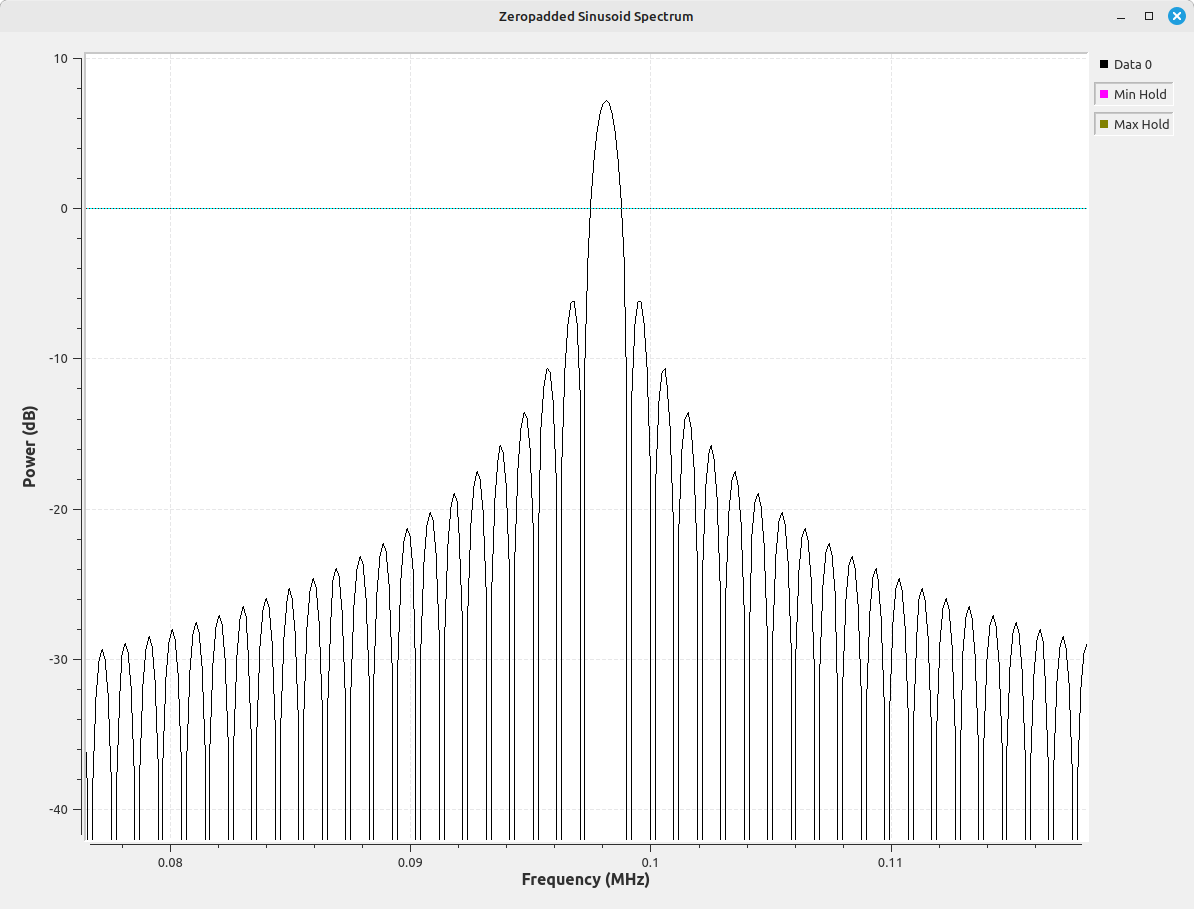
2D graph showing a group of thin lobes that peak in the center of the graph and fall away as they move towards the side. — Zoomed-in view of the zeropadded sinusoid. Note that the peak is now a curve and not flat.

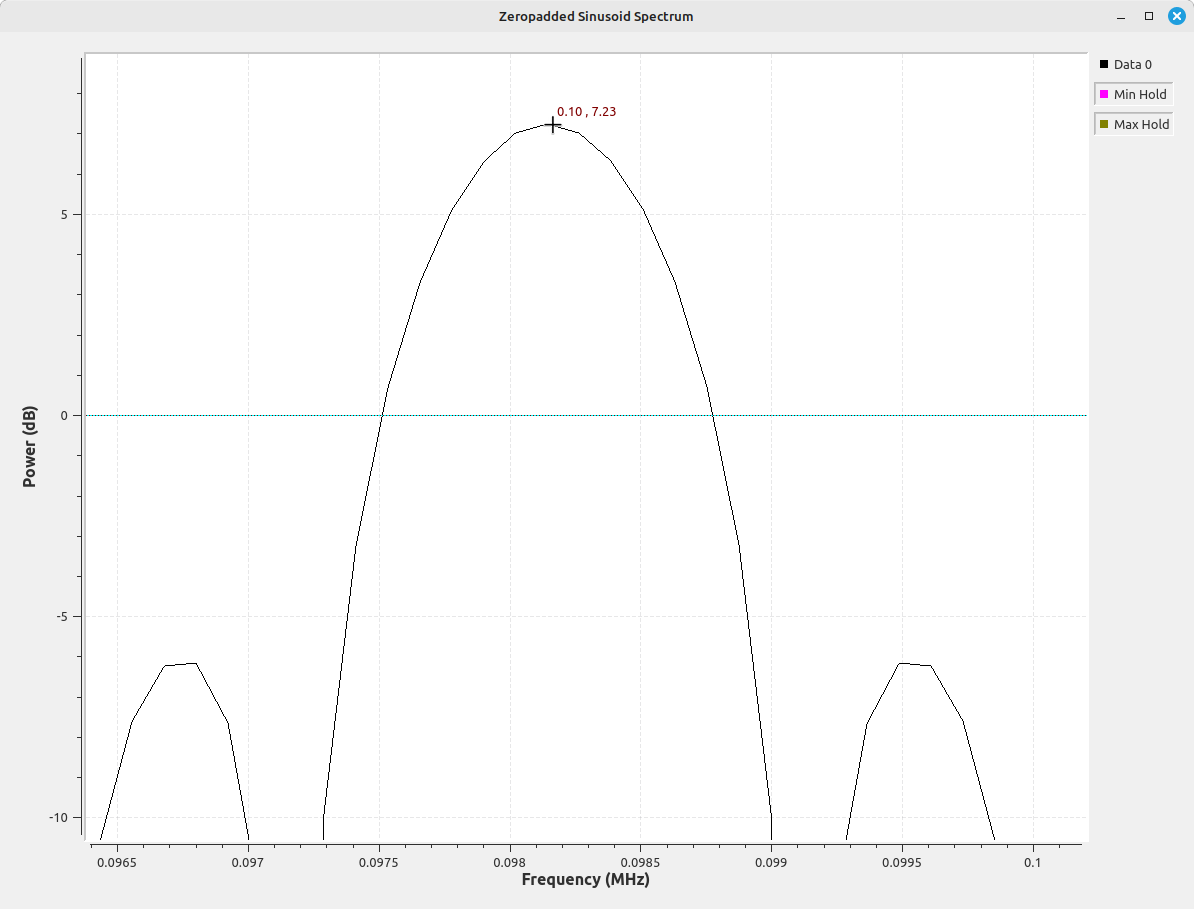
2D graph showing a thick lobe facing downward. There is a small plus sign at the peak. There is text next to the plus sign. — Zoomed-in view of the peak of the zeropadded sinusoid. Even though the sinusoid is at the edge of the frequency bin, the amplitude is accurate at 7.23.

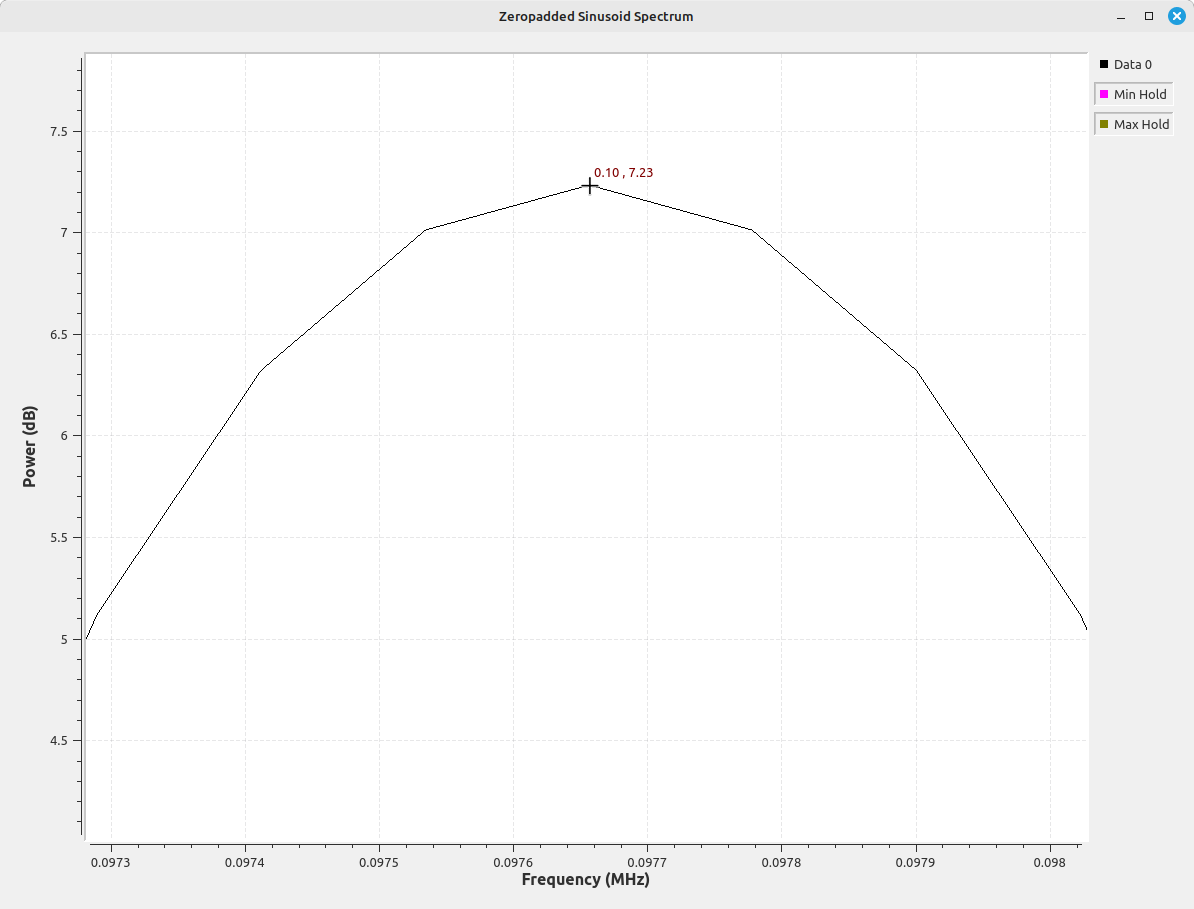
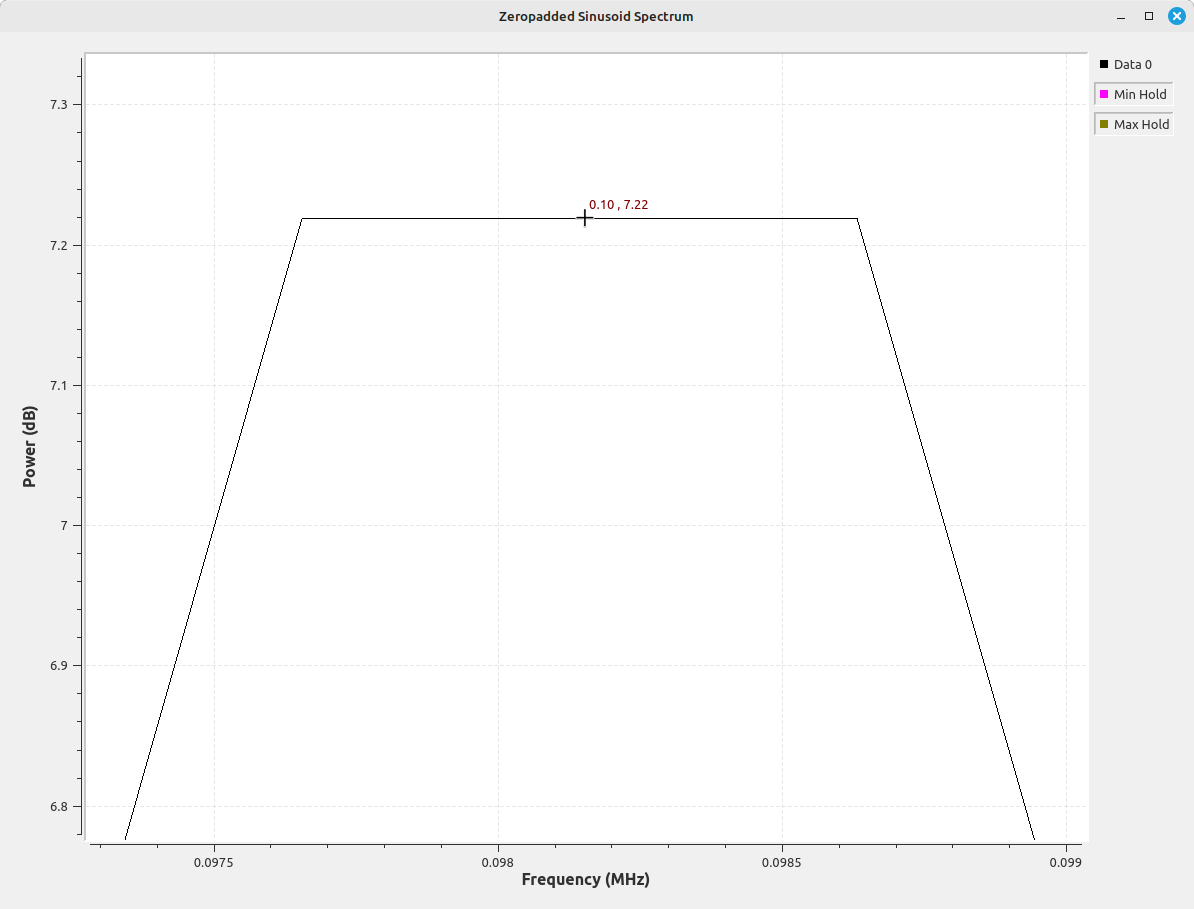
The display above shows that, with zeropadding of the time record, we can now accurately measure the power at the peak correctly. Further, with this technique, we'll accurately measure the peak, regardless of where the sinusoid winds up within the frequency bin, whether centered or at the edge. The image above was with the sinusoid at the edge of a bin. Below moves the sinusoid to the center of the bin.

2D graph showing a curve that starts in the lower, lefthand corner, rises to a peak in the center near the top of the display, and drops back down to end in the lower, righthand corner. A small plus sign with text next to it rests at the peak. — Measurement of the signal power using a marker at the peak. It is precisely the calculated value of 7.23 dB.

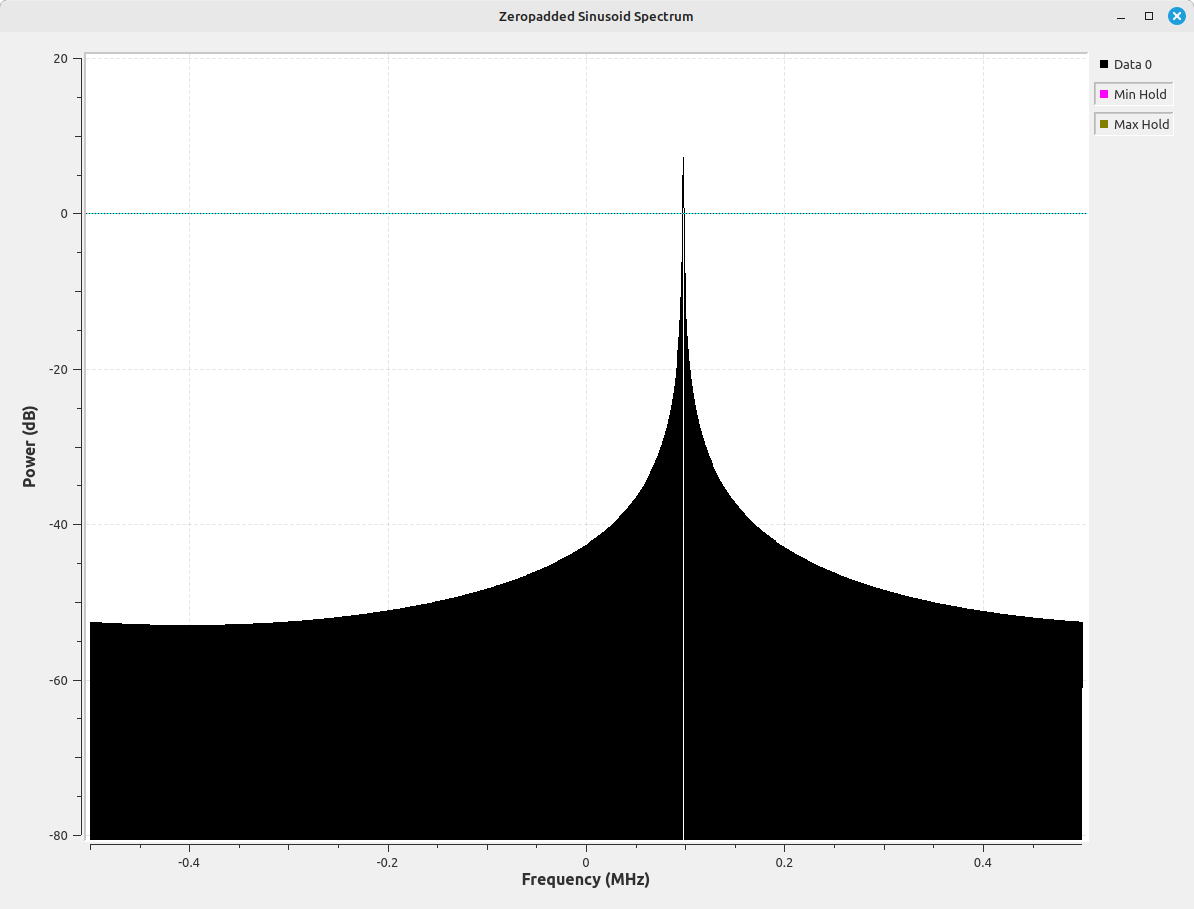
The downside to zeropadding is the extra processing required due to the increased size of the time record. There's the processing required to add the zeros, plus the extra processing within the FFT routine. All of the images above used a zeropadding of 8x, meaning that the time record fed into the FFT routine consisted of the original dataset plus a set of zeros that was 7x times the length of the dataset.

Flattop Window

Based on my limited experience, probably the most widely used method to limit spectral leakage, and the scalloping loss that comes with it, is the use of a flattop window. These are windows that are specifically designed to limit scalloping loss. Whereas the scalloping loss of an unwindowed (aka "rectangular / boxcar / uniform" window) data set can be as high as 3.92 dB, and even the Blackman-harris 4-term window (aka "BH92") has a scalloping loss on the order of over 0.8 dB, flattop windows typically provide scalloping loss on the order of 0.01 dB or less.

The downside is that this comes at the cost of a much larger resolution bandwidth (RBW). While most non-flat windows increase the RBW by a factor of 1.5 - 2, flattop windows will increase the RBW by factors of 3 - 5.

The one thing I want to emphasize here is that a "flattop" window is not a single window. Flattops are a family of windows that have the property of very low scalloping loss. The specific flattop window used in Gnu Radio Companion is the one provided by Stanford Research in their SR785 spectrum analyzer. It has a relatively high scalloping loss of 0.0156 dB. Regardless, the result is a very accurate peak measurement, regardless of where the sinusoid resides within the frequency bin (center or edge).

Block diagram showing three rows of blocks. The top row consists of half a dozen squares that are unconnected. The middle and bottom rows consist of roughly have a dozen blocks each that are connected by lines running from left to right. — GRC flowgraph to implement the flattop window. The correction for the peak power (the coherent power gain) is added in the "log10" block just before the QT GUI Vector Sink. For the specific flattop window used (the SR flattop), the correction value is 13.3 dB.

2D graph showing a trapezoidal figure with the base at the bottom of the graph. The top of the trapezoid, which is just above halfway to the top of the graph, has a small plus sign resting on it. The plus sign has text next to it. — This is the zoomed-in view of the peak of the sinusoid using the flattop window and with its center frequency set such that it is at the edge of a frequency bin. Even with that, the deviation from the actual value is only 0.01 dB, an almost negligble amount of loss.

Measuring Peak Power of Noise

Measuring sinusoids is all well and good, but what about noise? What does correcting for the coherent power gain of noncoherent energy do for the accuracy of our spectral display?

Let's find out.

I'm going to modify the flowgraph for the flattop window to add a noise source along with the signal source, as well as add averaging. We'll need averaging to reduce the variance of the noise so that we can make accurate measurements.

2D graph showing a roughly flat line running horizontally from left to right just below the middle of the graph. A vertical line extends up from this line almost to the top of the display. The vertical line is roughly 1/3 of the way from the righthand side of the graph. A small plus sign rests on the horizontal line at its center. A small bit of text sits next to the plus sign. — Spectral display of the noise and sinusoid averaged 10000 times. The marker measures the displayed average noise level (DANL) at roughly -40.72 dB. If we start with this value and correct for the ENBW, we get -40.72 -(10*log₁₀(3861.9)) = -40.72 - 35.66 = -76.38 dB. Given the rough measurement of the noise floor, this is tells us that using the coherent power gain on noncoherent signals lets us use the ENBW to accurately measure their power.

As I grew up on analog spectrum analyzers (the very first one I was ever allowed to touch and actually operate was a a Hewlett-Packard 8565A analog spectrum analyzer), those used the 3 dB points to measure the resolution bandwidth. As in "Tune the spectrum analyzer to an unmodulated tone, set the span so that it is just larger than the RBW, put a marker at the peak of the signal, drop down 3 dB to either side, drop a delta marker, then move the normal marker to the other side of the peak so that it is now equal in amplitude to the delta marker. The difference in frequency is the 3 dB bandwidth."

Pretty much every modern digital spectrum analyzer (meaning those that use the FFT) do not use the 3 dB points. They use the equivalent noise bandwidth or ENBW instead. While this makes it more difficult to compare measurements between analog and digital systems, turns out there are two good reasons for this change. They are:

Calculating the power spectral density: Using a measurement made using the coherent power gain combined with dividing by the ENBW, you can quickly calculate the power spectral density (PSD), even though that power represents noncoherent or incoherent energy. Once you know the PSD of the noise floor, you can quickly calculate the systems noise figure.
It's easy to calculate: I've already mentioned this story in another post, but I had the opportunity to ask fred harris if he knew why digital spectrum analzyers used ENBW as opposed to the 6 dB bandwidth (which would have been the equivalent to 3 dB in the analog systems). He just chuckled and said, "Because it's so easy to calculate." Which compared to measuring either the 3 dB or 6 dB points on a curve, calculating the ENBW is much easier.

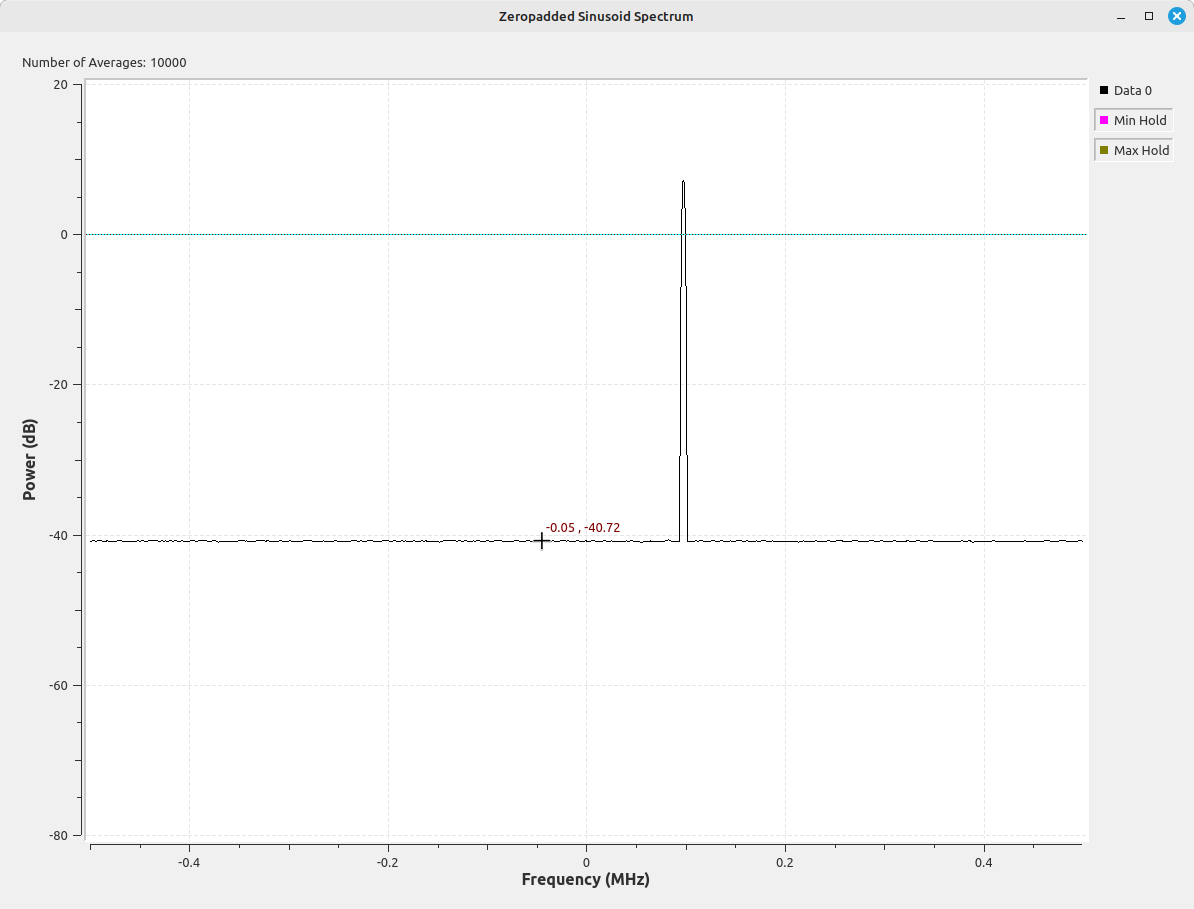
Getting back to our original problem, we have a measured DANL of -40.72 dB. Given the ENBW of our system of (1e6)(3.7702)/(1024) = 3861.9 Hz, this gives us a PSD of -40.72 - (10*log₁₀(3861.9)) = -76.38 dB. This is pretty close to our calculated value of -76.02 dB (especially given the crude method of measuring the DANL). If we take this measured value, add the bandwidth to it (10*log₁₀(1e6) = 60), we get -16.38 dB. This is equivalent to 0.0230 W, which is quite close to the actual value of 0.0225 (a difference of less than 3%).

Bottom line: Using a coherent power gain correction on our signals will give us accurate peak measurements plus allow us to calculate an accurate power spectral density of the resulting spectrum.

Measuring Band Power

Now that we've dealt with correcting spectrum amplitude measurements using peak power measurements, let's address using band power measurements. These are measurements where you can tell a system, "How much power resides between these two points on the spectral display?" For example, Signal Hound's Spike software allows for the measurement of all of the power within a band. (I'm also going to put in a plug for downloading this software even if you do not own any Signal Hound hardware. They provide a "Demo" mode that allows you to try out several features of their software without using any hardware.)

Screenshot of a spectral display in the center of the screen and takes up most of the screen. Different controls reside along the left, right, and bottom of the screen. On the graph itself, a line representing the noise floor runs horizontally from left to right roughly halfway down the screen vertically. — Screenshot of Signal Hound's Spike software operating in "Demo" mode. The spectral display is set to "Averaging" using 100 averages (exponential averaging). The marker is measuring the noise floor level. A band power measurement shows the power within the center 10 MHz of the 100 MHz span.

While I cannot say for certain precisely how Spike is making this band power measurement, my guess is that they're simply adding all of the power of each frequency bin within the markers. This would be a common method. Which leads to a problem if our points are corrected for coherent power gain. I've created a Gnu Octave script to perform a band measurement using a sinusoid windowed with a SR flattop window (since I've not been able to figure out how to perform a band measurement in Gnu Radio). I used coherent power gain, then switched to incoherent power gain. Here are the results:

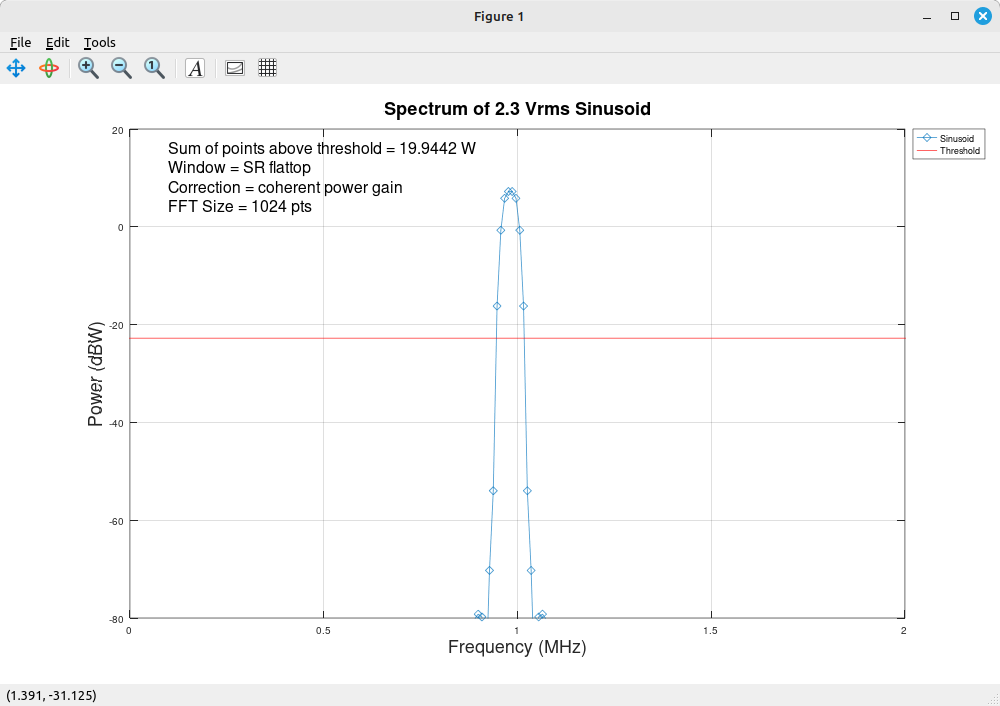
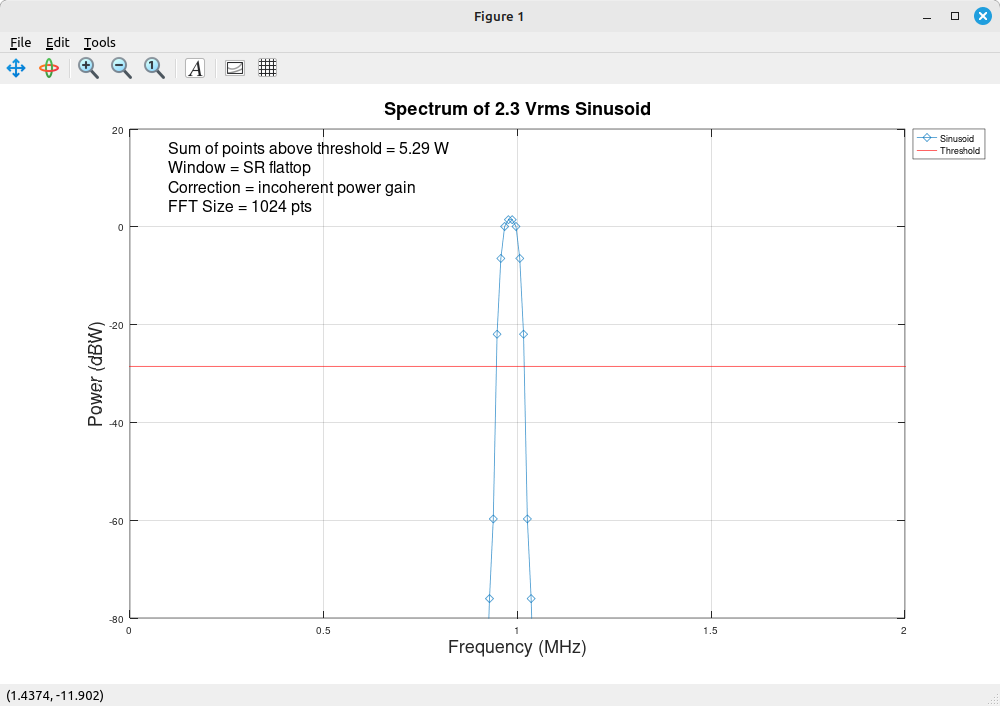
2D graph showing a thin half-oval shape rising vertically from the bottom of the screen. Along its circumference are small diamond shapes. A red line runs from horizontally the full width of the graph. Text resides in the upper, lefthand corner. — Spectral display created with Gnu Octave showing what happens to the band power measurement when each frequency bin has been corrected using coherent power gain. The script calculates a point 30 dB down from the peak of the sinusoid (a threshold denoted by the red line in the center), then adds the linear power of each point that resides above that threshold. It takes the sum and displays it in the upper, lefthand corner. The value displayed here, 19.94 W, is much higher than the actual value of 5.29 W. It's off by a factor of 3.77, *which precisely corresponds to the NENBW of the flattop window used to create the display.*

As noted in the captions above, the coherent power gain measurement using a band power measurement is high by a factor of 19.94 / 5.29 = 3.77. This corresponds precisely to the normalized equivalent noise bandwidth or "NENBW" of the flattop window used to create the spectral display. Hence, if we have a display that is created using the coherent power gain but we want to make a band power measurement, we need to take the measured band power and divide by the NENBW of the window used when creating the display. Another option is to use the incoherent gain for correction when creating the spectral display. This will provide an accurate band power measurement with no further processing required.

Using the incoherent power gain gives us accurate power/bin, while coherent power gain gives us accurate power/Hz. As an example, I'm going to modify the flowgraph that I used to measure the noise spectral density so that it uses the incoherent power gain rather than the coherent.

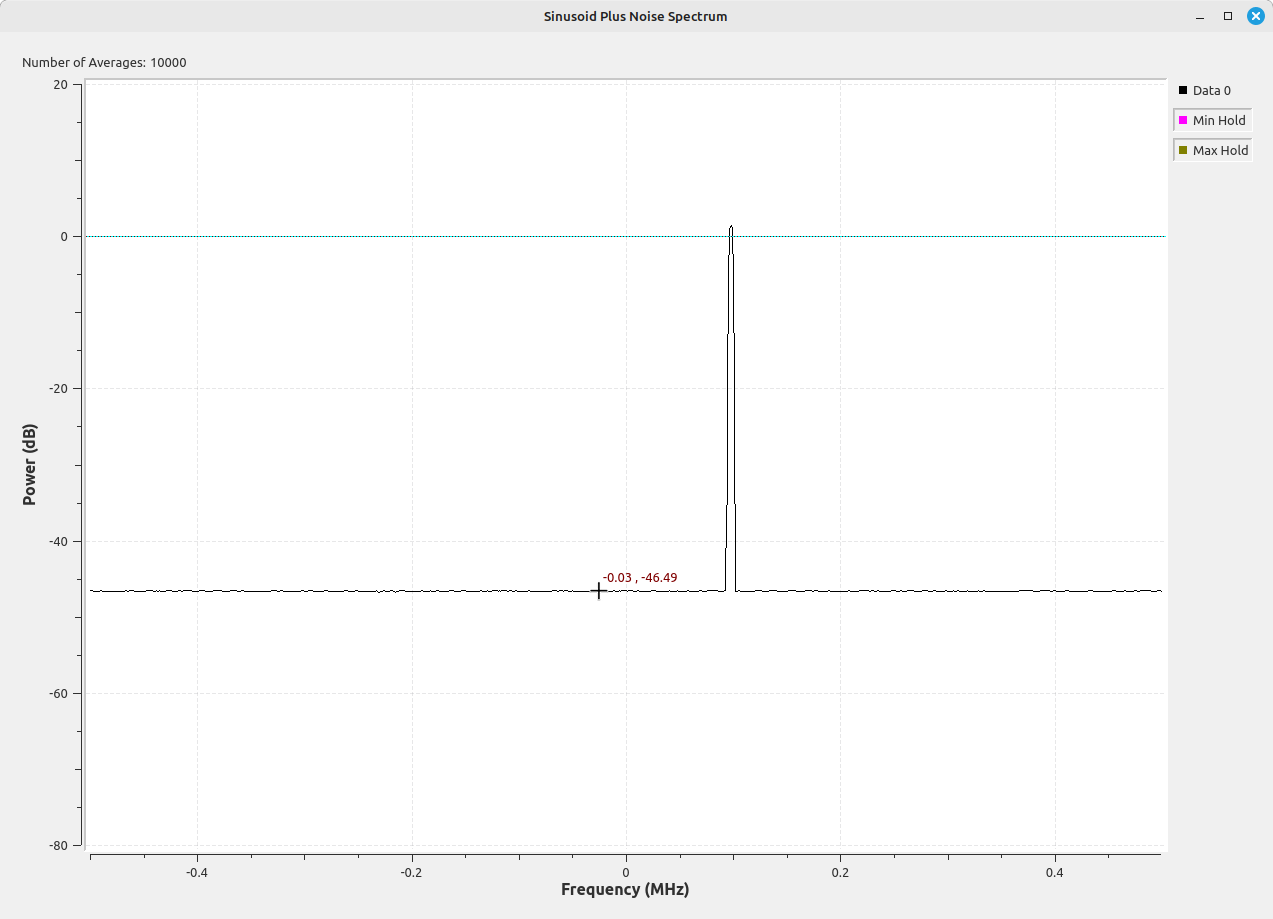
The displayed spectrum shows a noise floor that is lower by 5.77 dB (-46.49 - (-40.72) = -5.77 dB) than that measured using the display corrected with the coherent power gain. This difference is due to the NENBW. The window used for this display was the SR flattop, which has a NENBW of 3.77. In dB, this is 10*log₁₀(3.77) = 5.76 dB. What this measured value is showing you is the power per frequency bin. With this measured level and knowing the number of frequency bins (1024), we can calculate the total power level. Given the measured level of -46.49, the total power is -46.49 + 10*log₁₀(1024) = -46.49 + 30.1 = -16.39 dB. Again, this corresponds to a total noise power of 0.023 W. The calculated value is 0.0225, a difference less than 3%.

Switching Between Values

Which brings us to a conclusion we can make about all of these correction values. We can use any of them we want for display (peak or band) and convert to the other using the NENBW as the conversion factor. I'm just going to create a short list of the differences.

When using...	... you get...	... which can be converted to the other by
Coherent power gain	power/Hz	dividing by the NENBW
Incoherent power gain	power/bin	multiplying by the NENBW

As an example, let's say that I have my display setup using the coherent power gain (peak power), but I want to do a band power measurement. I would make the band measurement, then divide by the NENBW of the window to achieve the correct band power measurement.

The Problem with Averaging

I want to finish up this post by making a measurement of an actually-modulated signal using all of this new-found knowledge. But before we do that, we have to talk about "the problem of averaging". This is a problem that exists with noncoherent or incoherent energy and the use of logarithmic scales used in spectral displays. Refer back to my flowgraph for creating a spectral display using averaging. Notice that the block that performs the averaging is separate from the block that performs the logarithmic conversion ("Log10" block). Since these are two blocks, they can go in two orders. The first is as shown, meaning average then convert to decibel. The second is to first convert to decibel then average. Let's find out what happens if switch them around. I'm also going to switch the power gain correction back to coherent power gain.

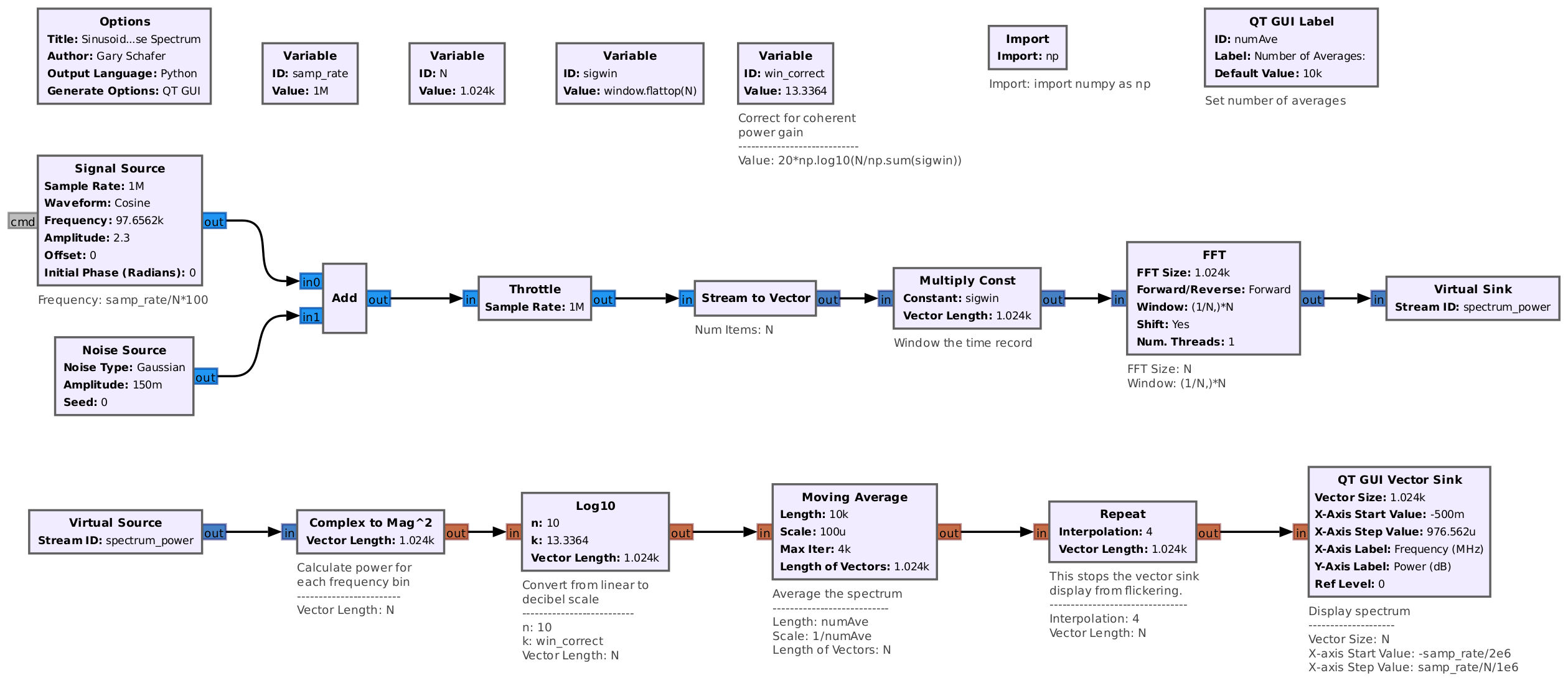
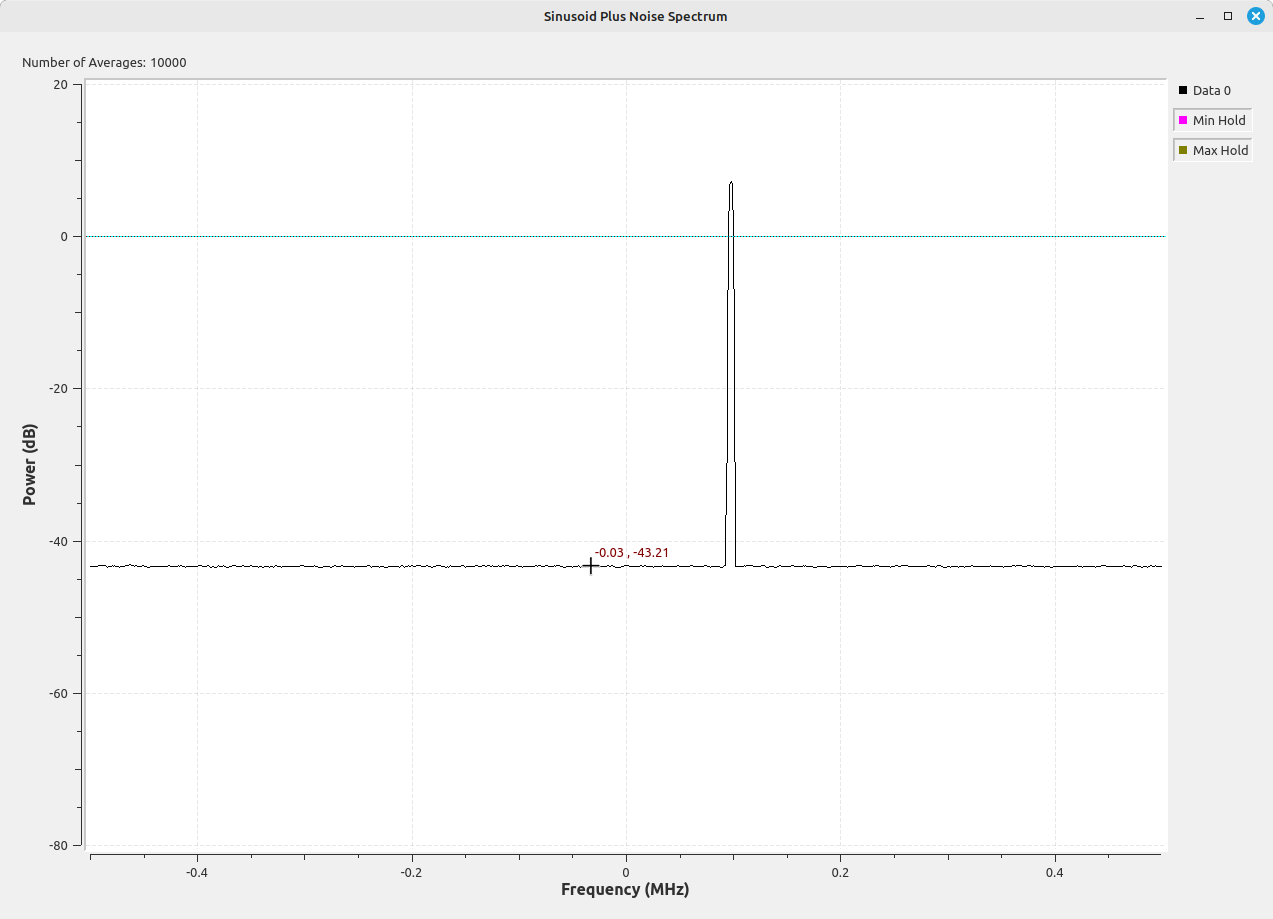
Looking at the spectral display above, we have a measured noise floor (using coherent power gain correction) of -43.21 dB. This is different from the previous display in which the averaging was performed first (using linear values) then converted to dB. That value was -40.72 dB. This is a difference of -2.5 dB. This difference is due to the inherent skewing of log scale amplitude values. What this means is that, if you're using a display that first converts to log scale and then averages and you're measuring a noncoherent / incoherent signal (noise, for example), you have to add 2.5 dB to the measured value.

The Gnu Radio QT GUI Frequency Sink is one of those systems that averages log scale values rather than linear. This means that, if you're trying to measure power levels of noncoherent signals using this block, you have to add 2.5 dB to the measured value plus the desired power gain correction factor (coherent or incoherent).

And in case you're curious as to why this was not solved in the first spectrum analyzers, those first analyzers were analog, and the use of a log scale was part of the conversion to spectral data. It literally was not possible to average before converting to the log scale. The upside was that, once the switch to digital occurred, most people realized, "Hey, let's move that averaging to before the decibel conversion, shall we?"

Measuring a Modulated Signal

These measurements of noise and sinusoids is all well and good, but what about measuring on modulated signals? Signals that have some bandwidth to them? Measuring band power in Gnu Radio is not something I've figure out how to do yet. So I'm going to model it with Gnu Octave. I've created a script that will create a basic FM signal (modulated with a sinusoidal tone), then sum the power of each point between two frequencies.

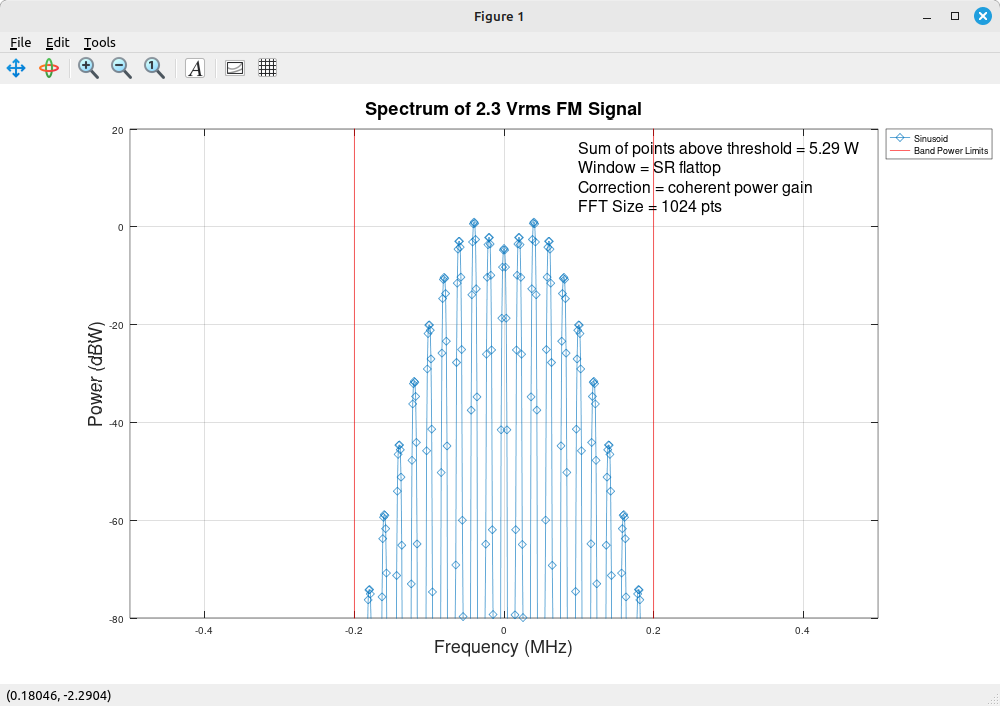
2D graph showing a group of vertical lines at the center that are randomly covered with small diamonds. The group starts at the bottom just left of center, rises towards a peak at the center (with the peak just above halfway between bottom and top) and then drops back down to the bottom just to the right of center. Two red lines at the edges of the grouping extend from top to bottom vertically. Some text sits in the upper, righthand corner. — Spectrum of the FM signal. The red lines indicate the limits of the band power measurement. The script sums each frequency point within those limits. The amplitudes were corrected using the coherent power gain, but the band measurement was then corrected from these values by dividing by the NENBW of the window (a SR flattop with NENBW = 3.77). The final measured value is precisely the calculated value of 5.29 W.

Which worked quite nicely. I actually used the coherent power gain for correcting the spectral amplitudes, then once I'd calculated the band power, I divided it by the NENBW. The resulting measured power is quite accurate.

Yay, us.

Summary

And I'm spent. Let me add one, last statement. There's a third method for making band power measurements. That is filter out the desired band and measure in the time domain. Frankly, given everything I've just covered, this might just be easier and much more fool-proof.

Through this post, I hope that I've allowed you to understand some of the pitfalls and "gotchas" of spectral power measurement. Measuring power, regardless of source, using spectral data requires care and understanding of what those amplitudes represent (and how they were created!)

References

[1]"On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform", fred harris, Proceedings of the IEEE, Vol. 66, No. 1, January 1978.

Random Quote Board