

Random Quote Board
Digital AM Demodulators
Since I've taken such a deep look at the various forms of frequency demodulation, it's time to pay some attention to that other primary analog modulation method, amplitude modulation (AM). Rick Lyons put together a post on "Digital Envelope Detection". I'm going to build these different demodulators and see how well they work with Gnu Radio.
Amplitude Modulation Review
Let's do a quick review of amplitude modulation. It's one of the three types of sinusoidal modulation. The other two are frequency modulation (FM) and phase modulation (PM). The carrier, as always, is a sine wave. The envelope of a sinusoid is the difference between the maximum and minimum of the instantaneous amplitude of it.
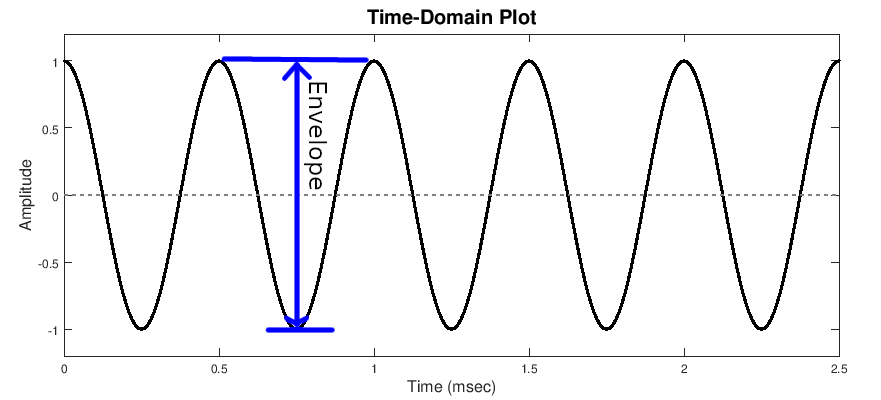
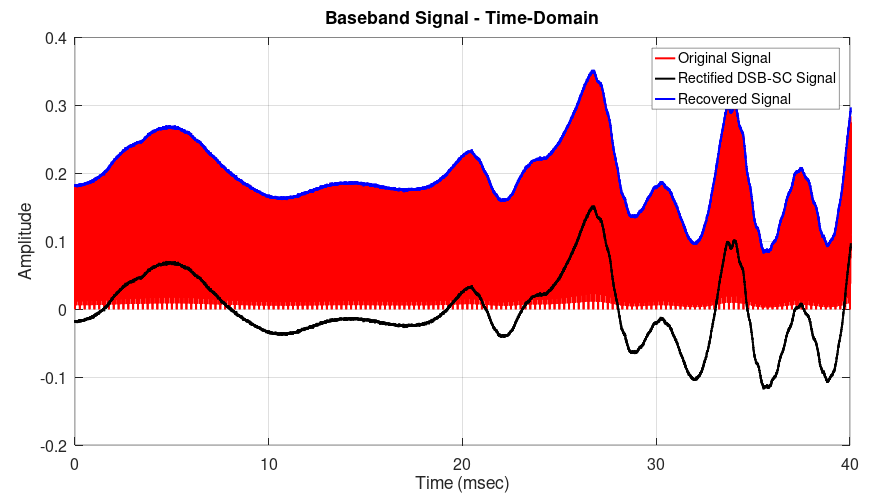
Amplitude modulation varies this envelope, as shown below.
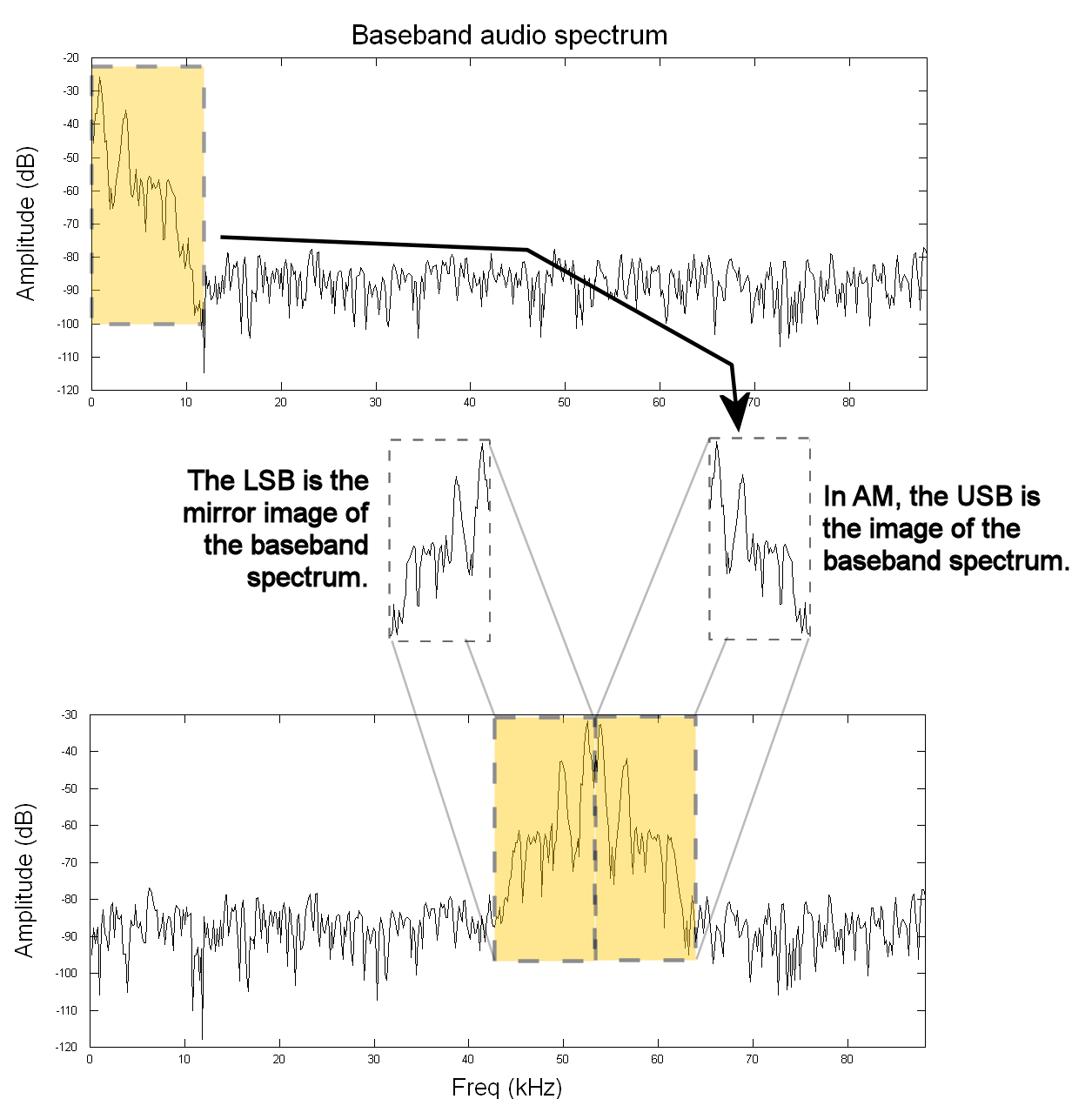
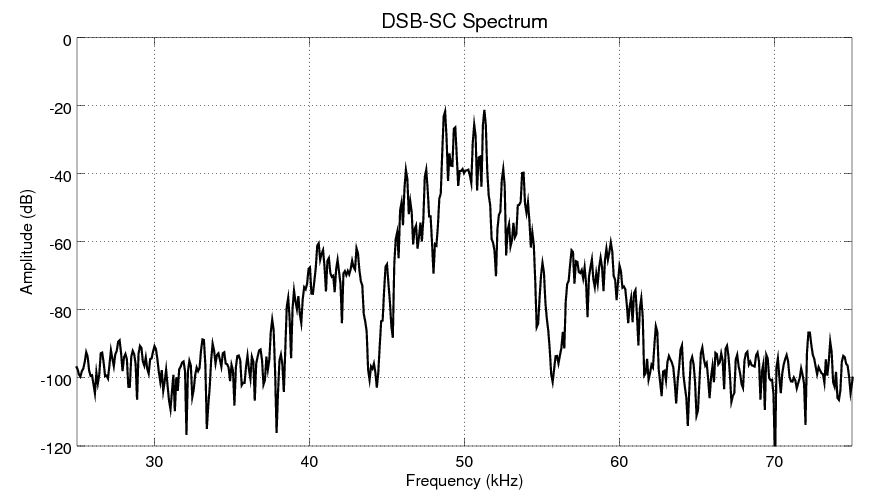
From a frequency viewpoint, AM carries the information in sidebands. When we look at the spectrum of AM signals, we have (up to) two sidebands, an upper sideband (one higher in frequency than the center frequency) and a lower sideband (one lower in frequency than the center frequency). Each sideband contains all of the information of the original signal. As a matter of fact, each sideband is the original signal, simply frequency translated up to a higher frequency and (possibly) frequency inverted.
Amplitude modulation (AM) can be broken down based on two parameters. These are:
- Carrier level: There are three levels for the "carrier" in AM signals. These are "full", "reduced" (or "residual"), or "suppressed". I've always disliked the use of the term "carrier" in this context. There is no such thing as a "suppressed carrier" signal. That's the same as "no signal". You have to have a carrier in order to have a modulated signal. What we're talking about here is the presence of a tone at the carrier frequency. That tone is a reference, meaning it is in phase with the modulated signal and can be used to demodulate the AM signal. So, when people say "suppressed carrier", what they really mean is "suppressed reference". And that means that the receiver needs to recreate the reference in order to successfully demodulate the signal.
- Sideband presence: In AM, the information is contained in sidebands. There can be a sideband above the carrier frequency, and one below the carrier frequency. A signal can be "double sideband" (DSB), "single sideband" (SSB), which can be further divided into "lower sideband" (LSB) or "upper sideband" (USB), "vestigial sideband" (VSB) and "independent sideband" (ISB).
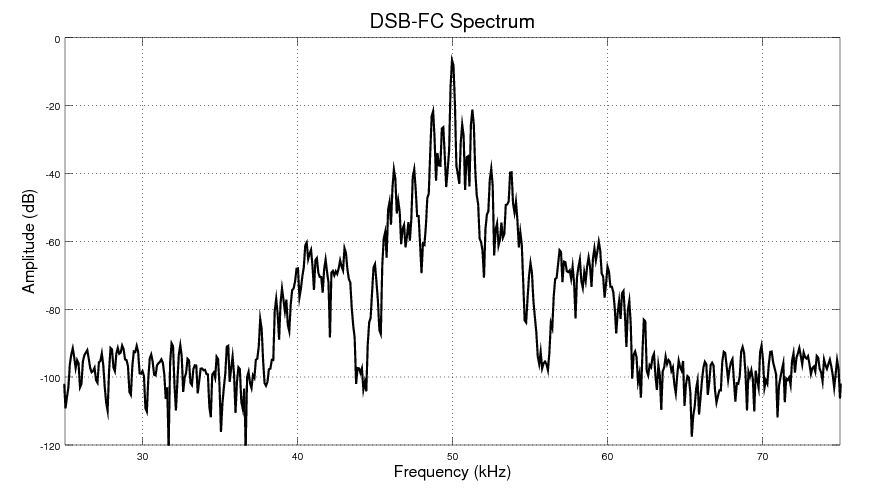
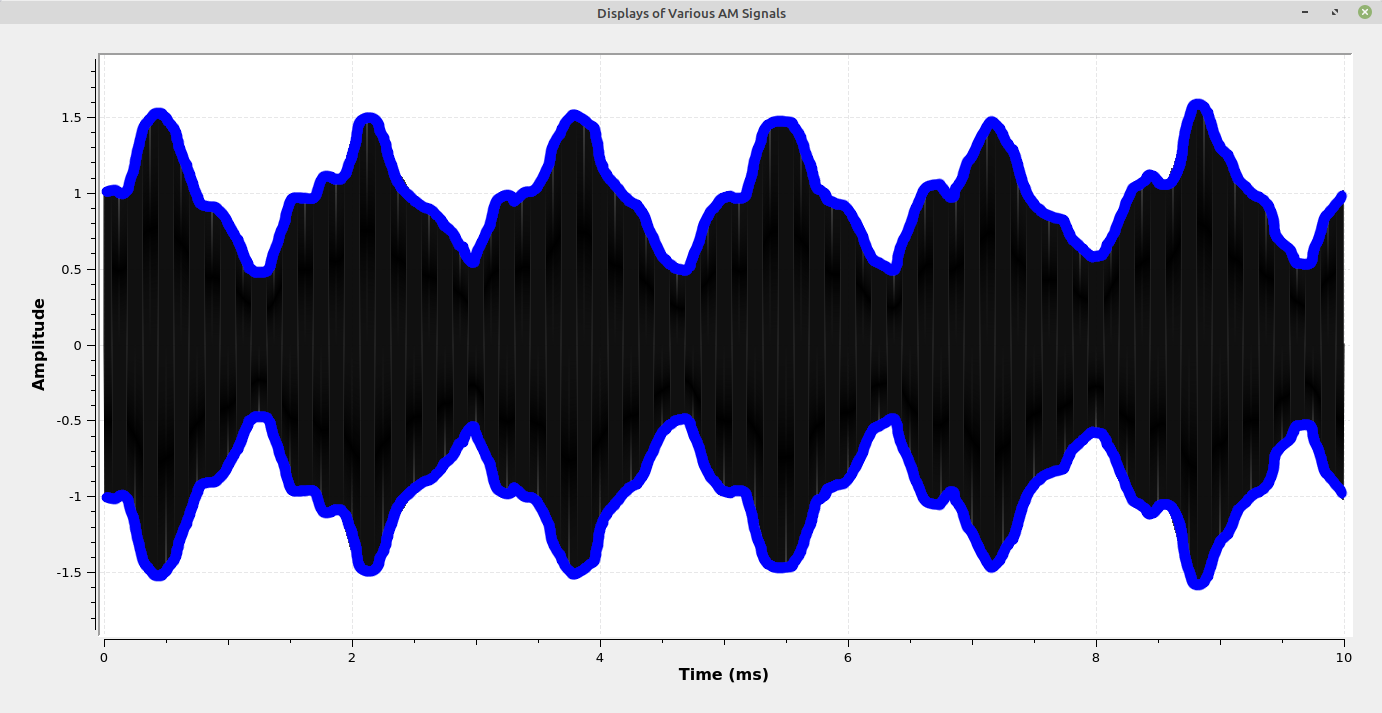
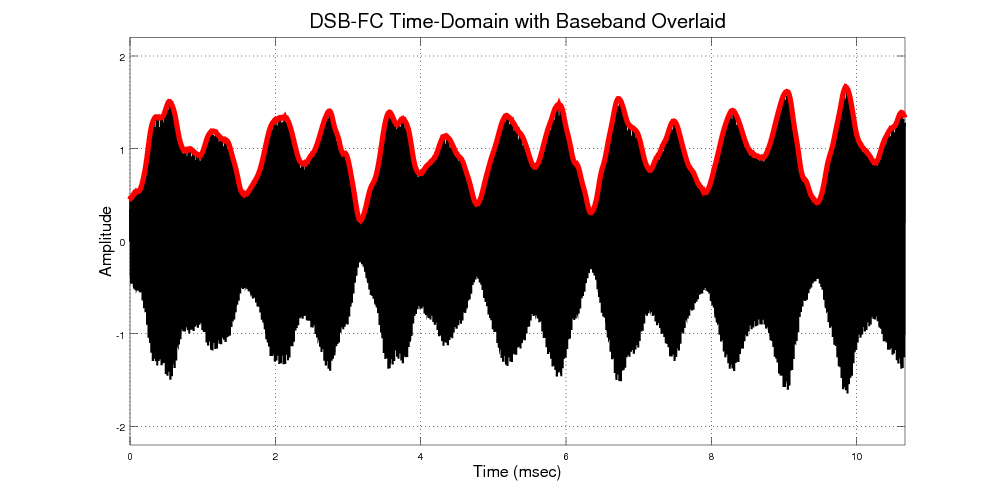
The images below show the difference between suppressed and full carrier in the time domain. In a full carrier AM signal, the upper and lower edges of the envelope will not cross the zero line. In suppressed carrier, the envelope will cross the zero line.

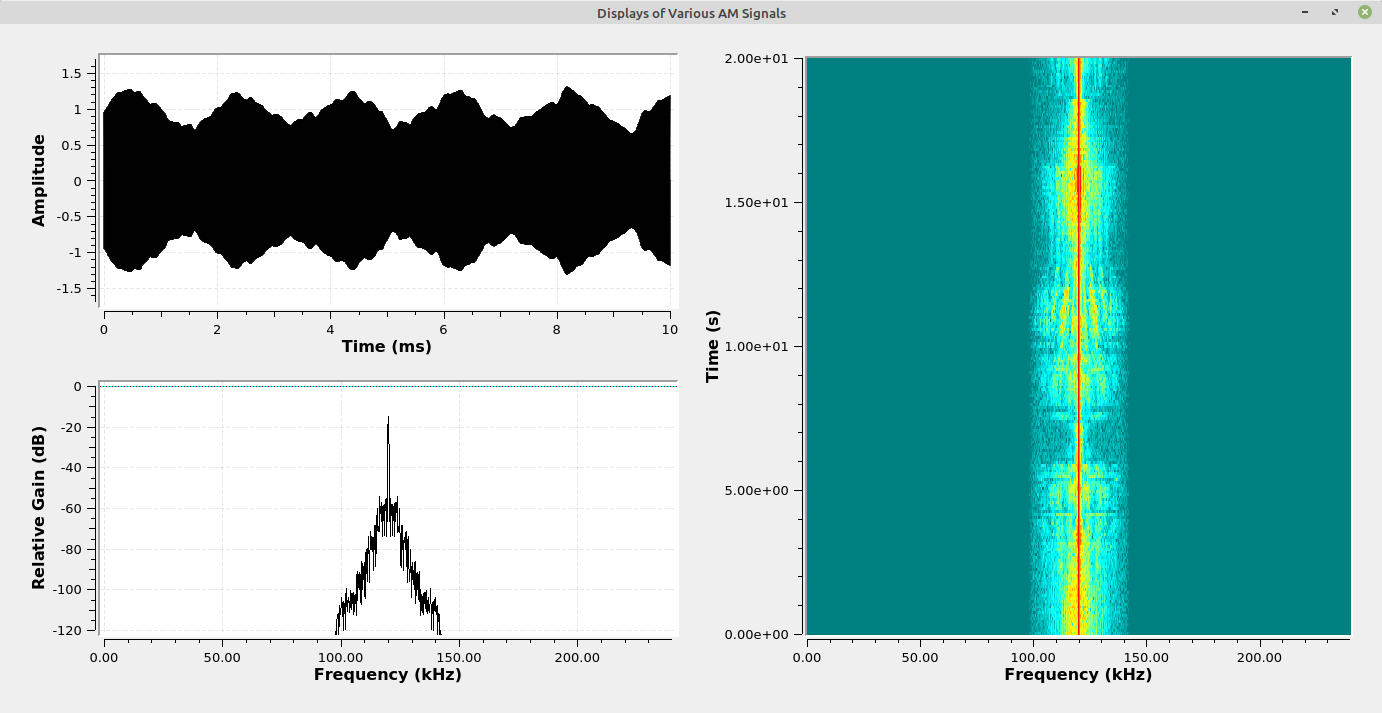
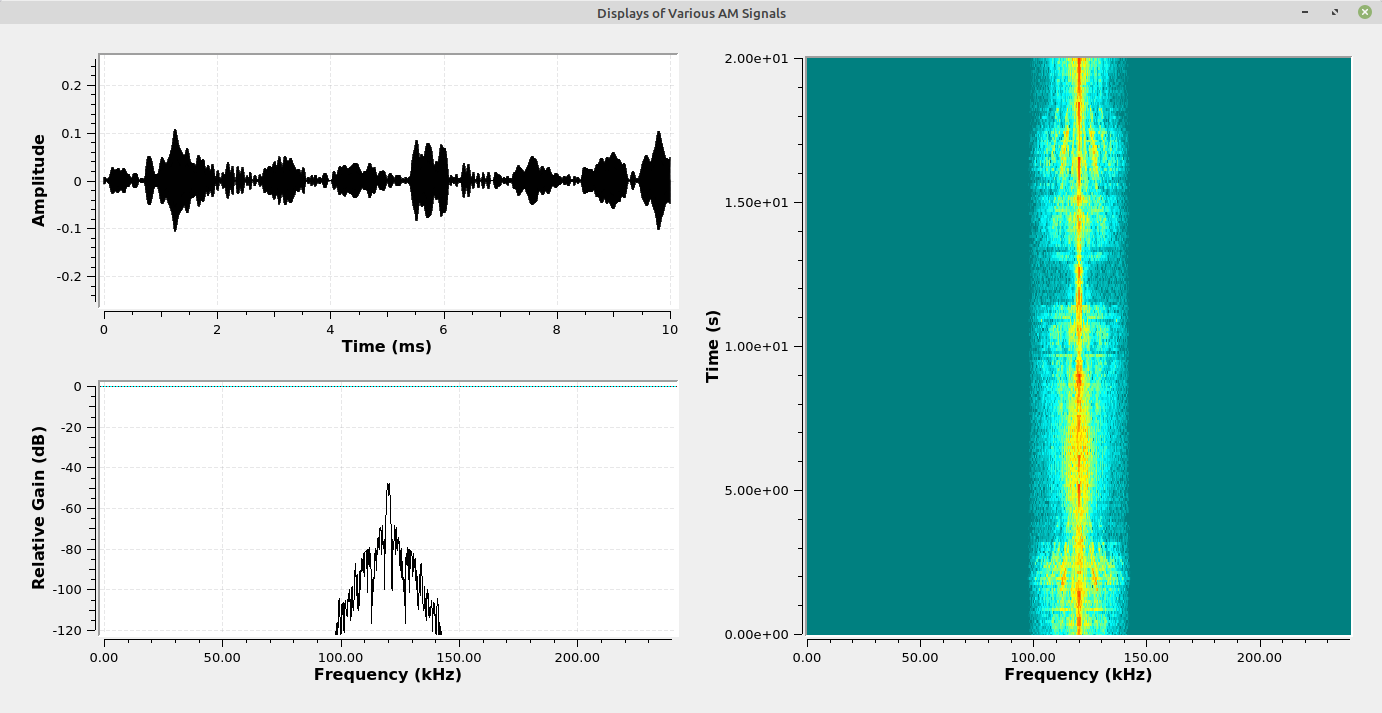
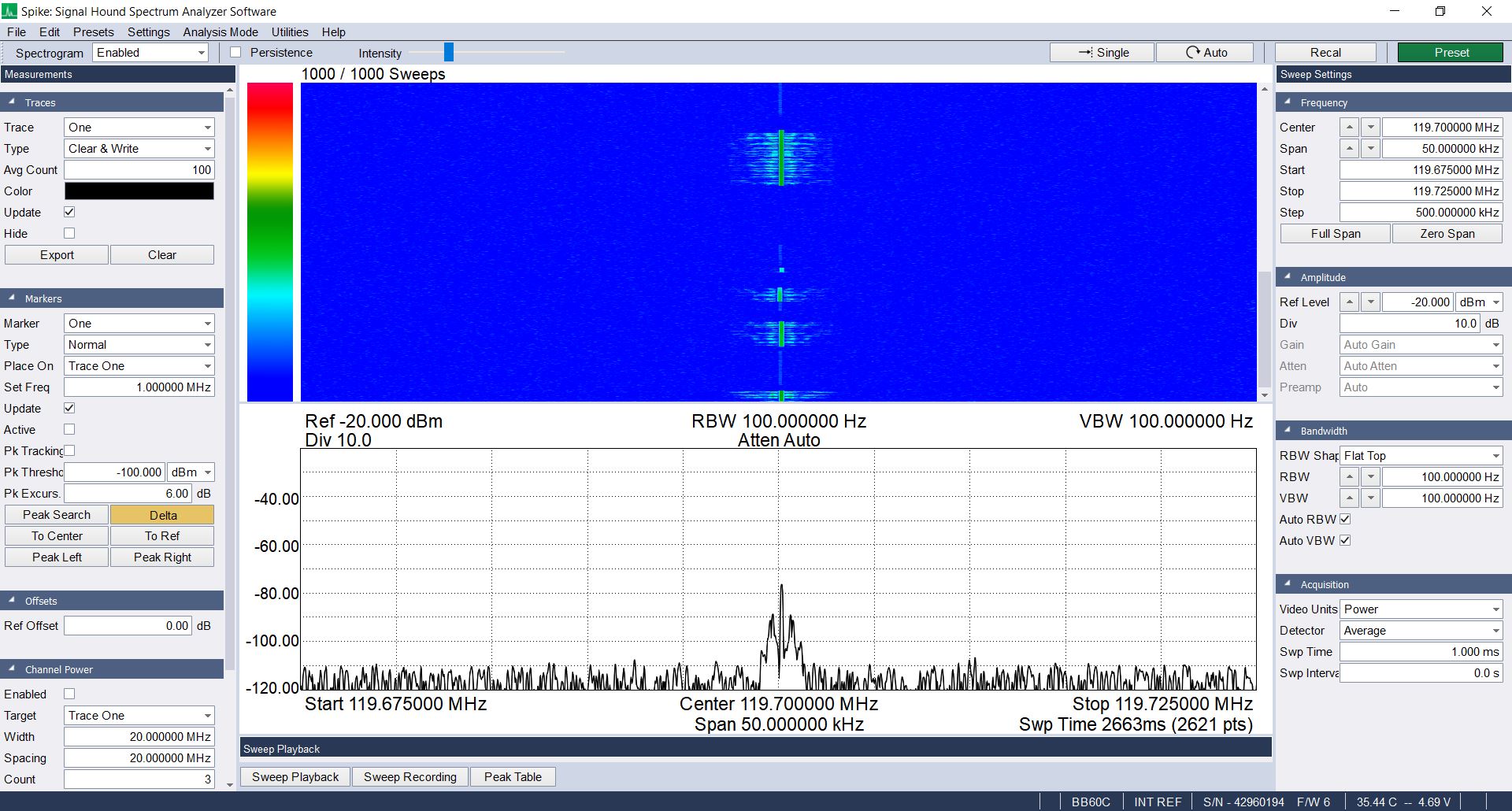
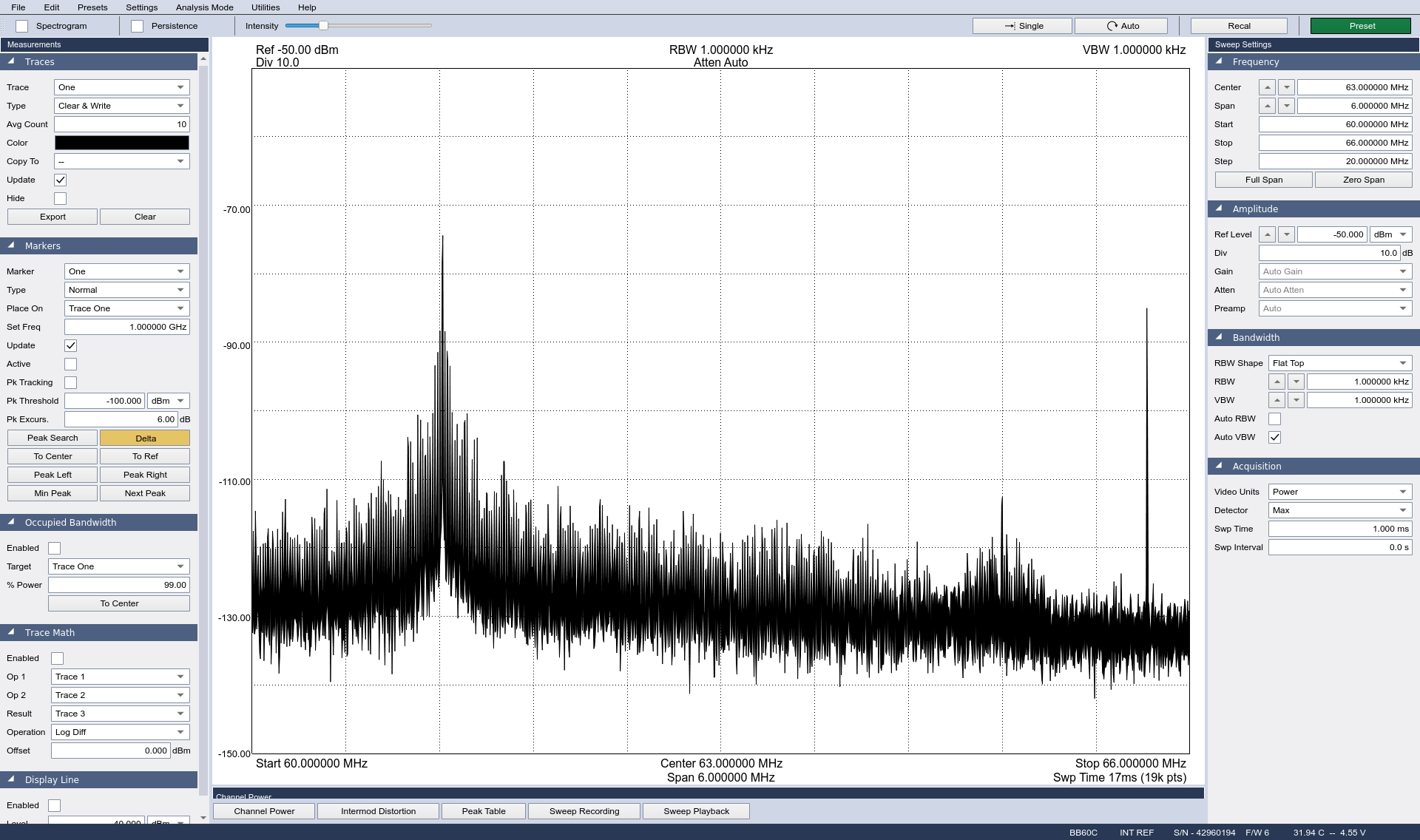
The following images show various facets of the different "flavors" of AM. For each image, the upper left display is the time domain showing the amplitude variation of the carrier. The lower left display is the spectral trace, while the right display is the spectrogram of the modulated signal.
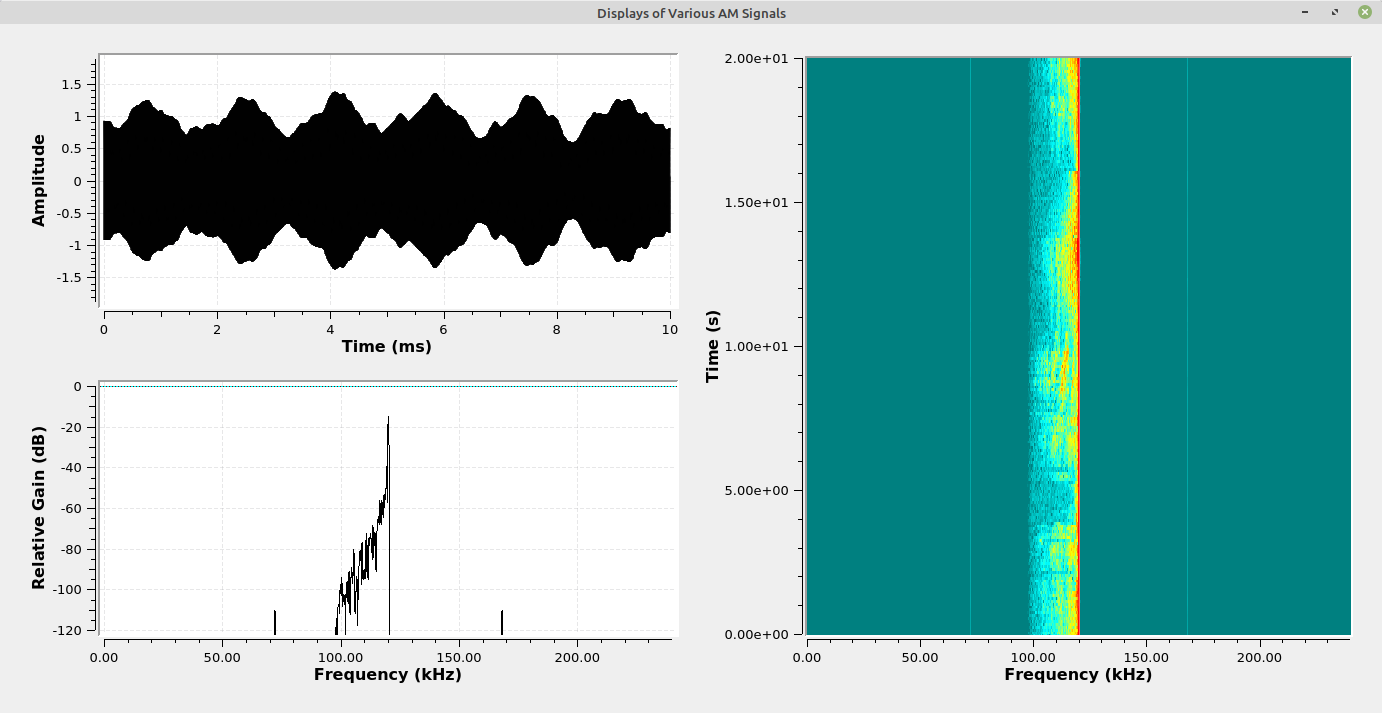
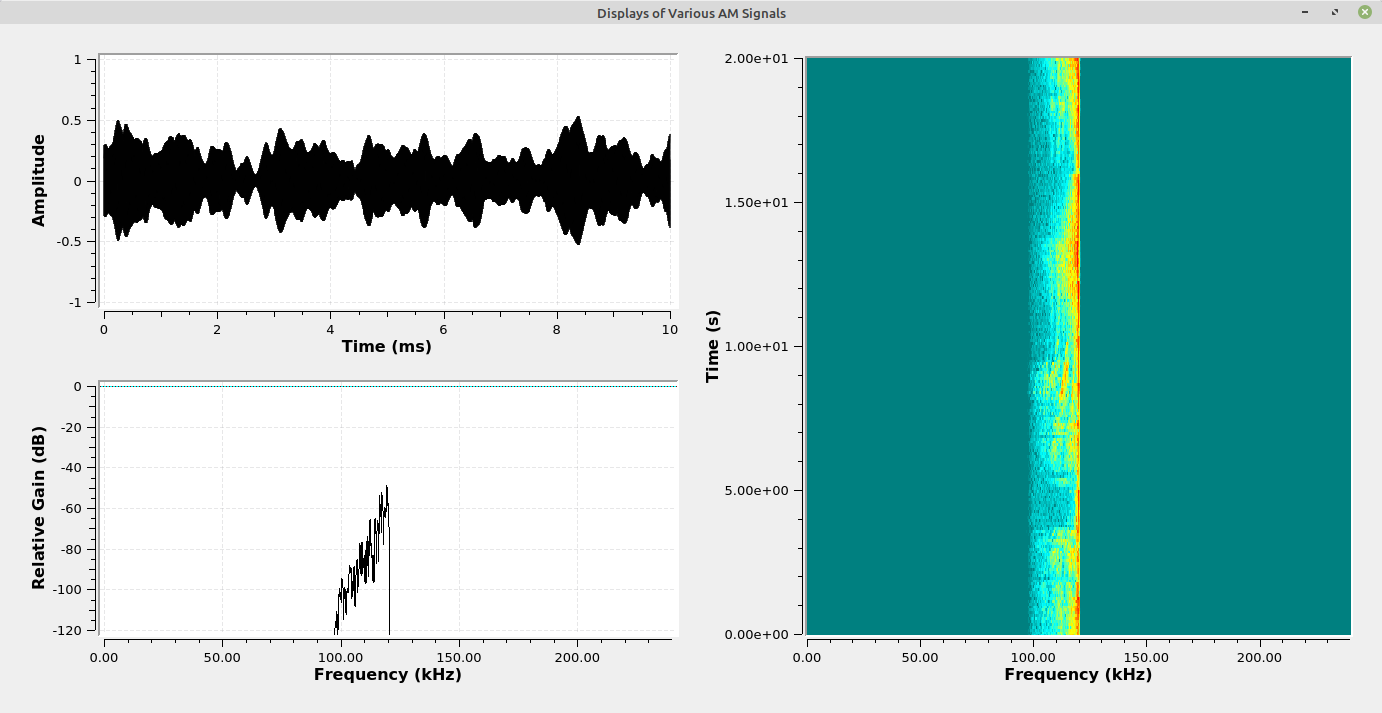
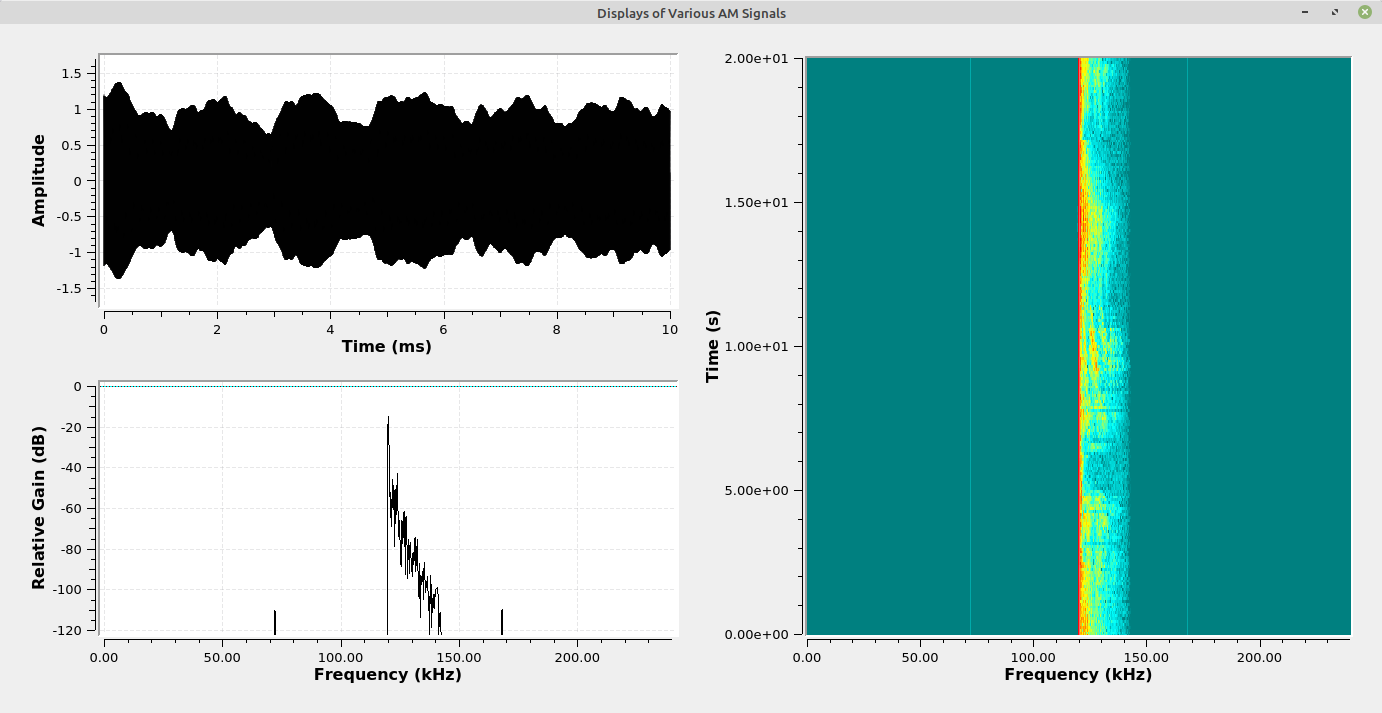
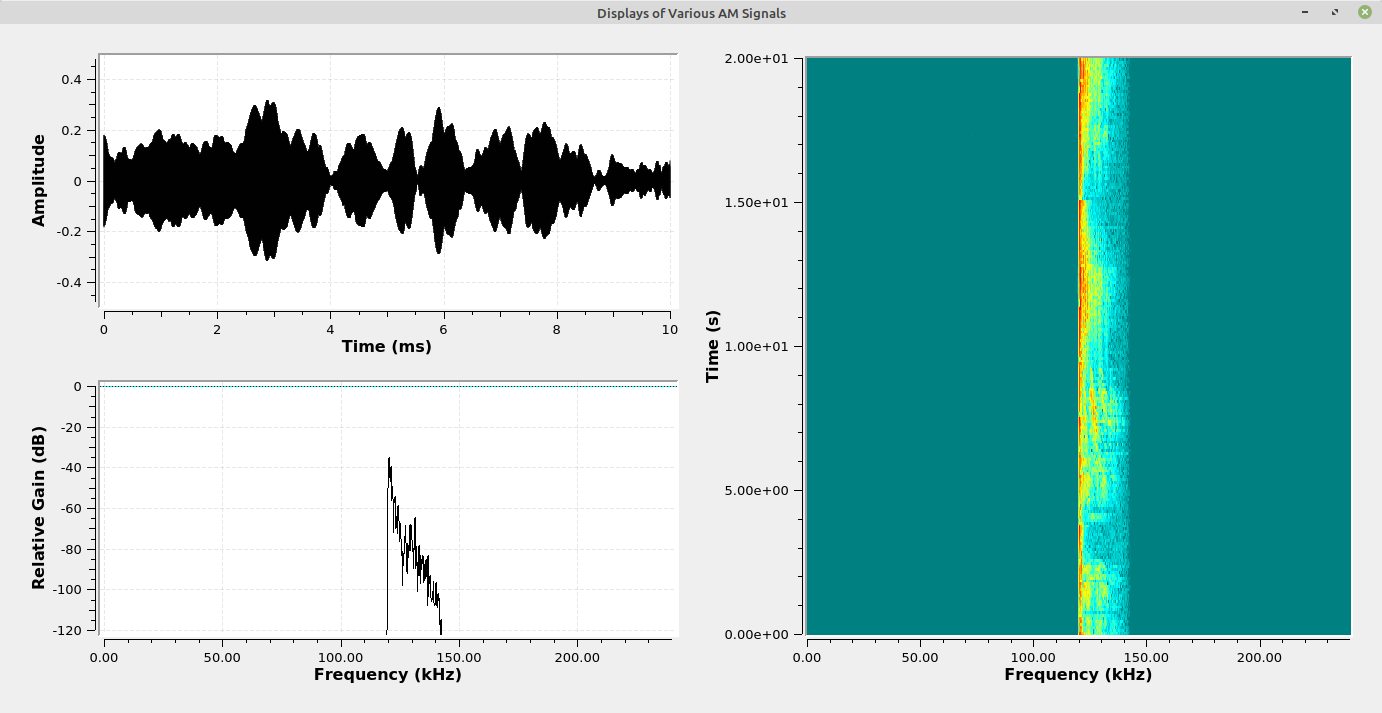


Amplitude Demodulation
Amplitude demodulation is the method we use to extract the original information from the modulated carrier. As the information signal varies the envelope, amplitude demodulation refers to extracting the envelope in order to recover the information.
General Methods of Demodulation
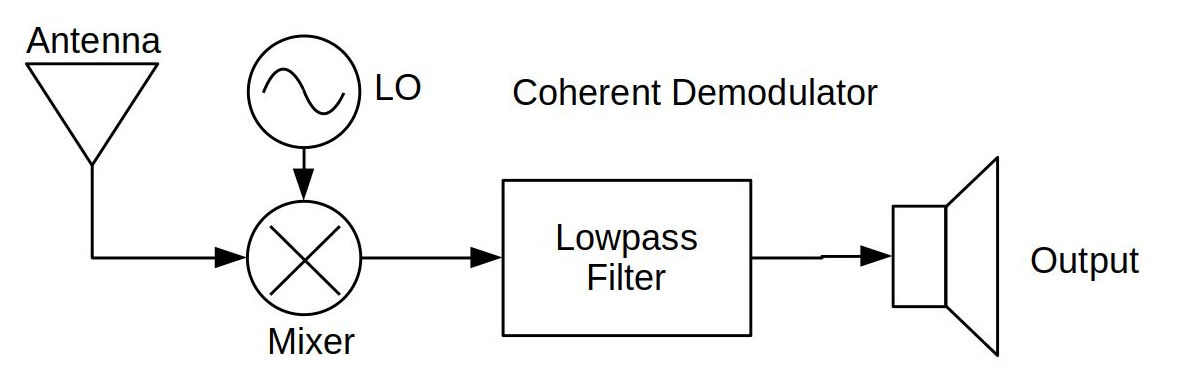
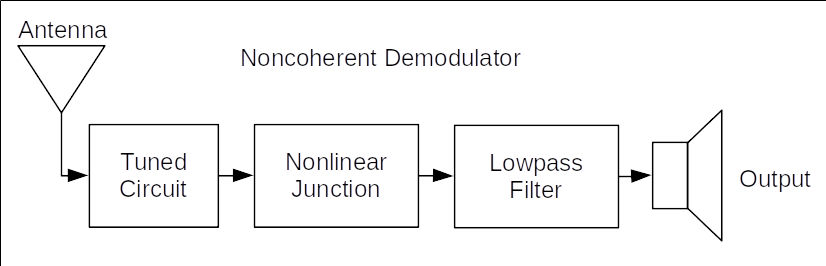
There are two, general methods for amplitude demodulation. These are noncoherent and coherent. Lyons's paper refers to this as asynchronous and synchronous, respectively. This refers to whether a sinewave in phase sync with the AM carrier is required. It's not required in the case of noncoherent / asynchronous, and required (sort of) for coherent / synchronous.
In his article, Lyons discussed several, different types of information that might be used. For example, he talked about amplitude shift keying (ASK, or amplitude modulation with digital bits as the information signal), basic analog audio, and medical electromyograms (EMG). For this post, I'm going to use simple audio signals, double sideband full carrier and suppressed carrier.
For all of the noncoherent demodulation methods, I'm going to use a double sideband full carrier signal.
Noncoherent Amplitude Demodulation
There are three general circuits for noncoherently amplitude demodulating a signal. All three perform the same basic function. They all remove the negative half-cycle of the modulated waveform. One circuit (half-wave rectified) simply removes the negative (or positive, depending on the polarity of the diode) portion of the time domain waveform. The other two circuits (full-wave rectified, squaring) convert the negative to positive amplitudes.
In this case of a full carrier system, this is not a problem. As seen below, with noncoherent demodulation, we've not affected the information. Noncoherent won't work with suppressed carrier due to the fact that the rectification process (regardless of how it is performed) will distort the original information signal.

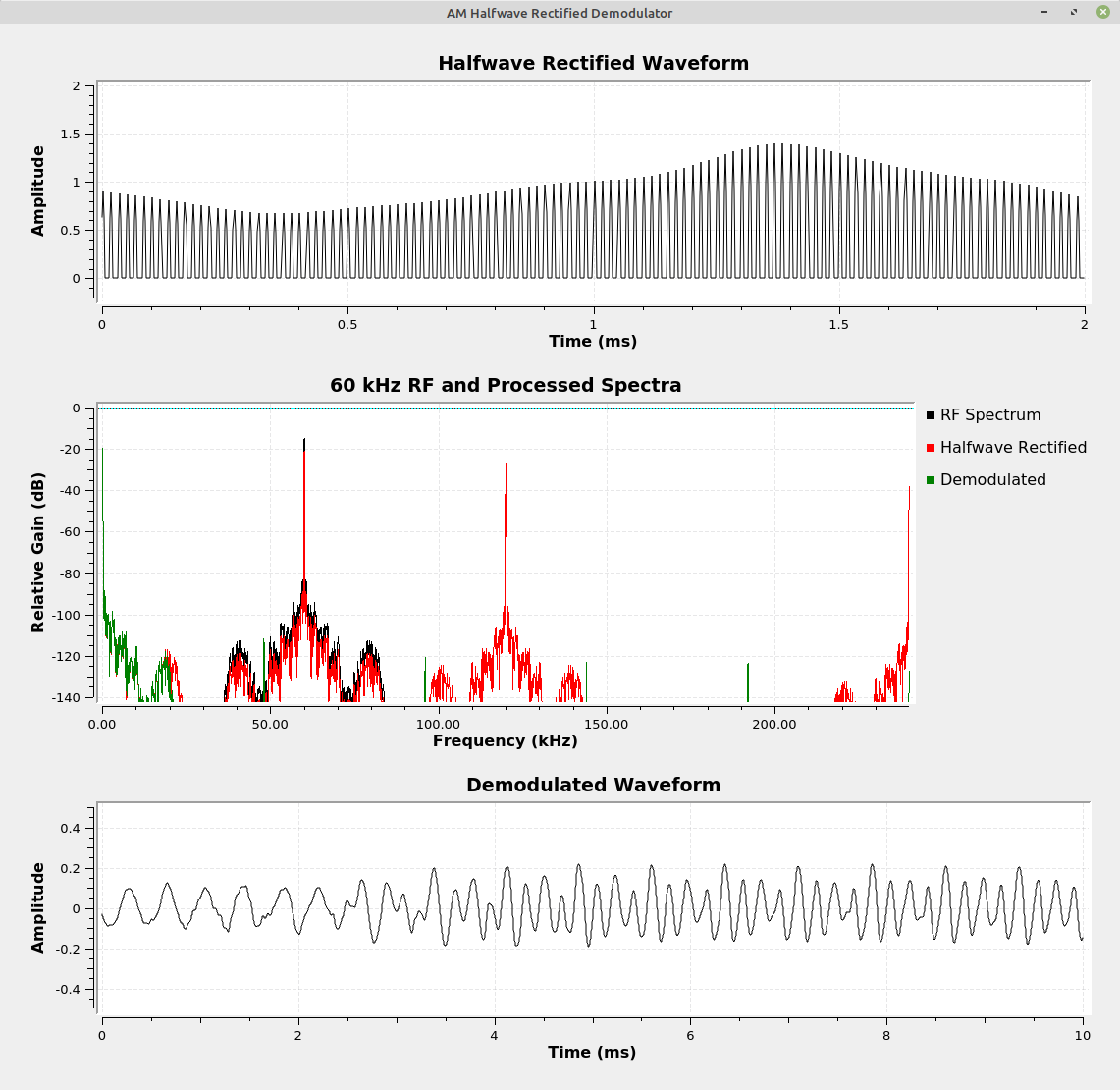
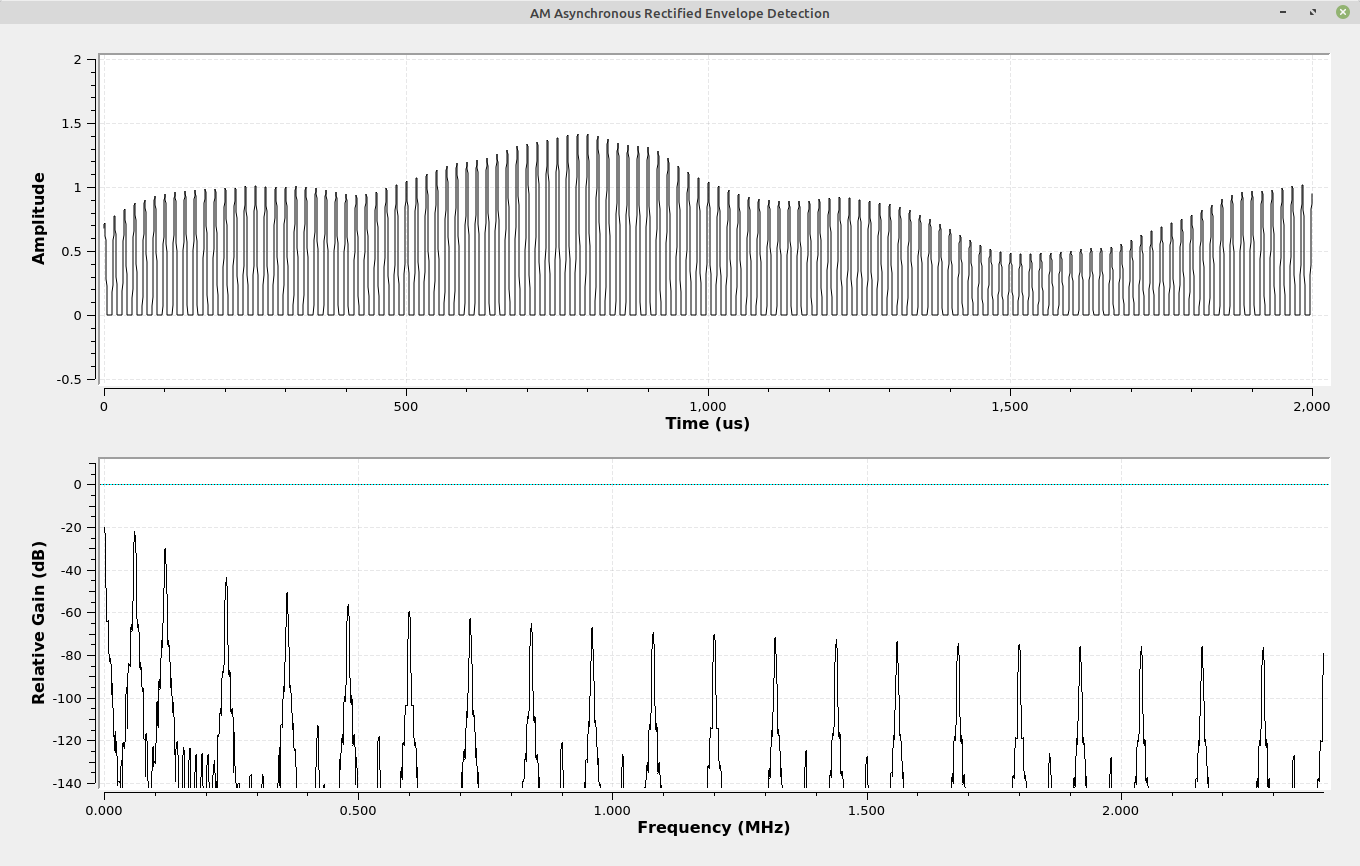
Half-wave Rectified Envelope Detection
Lyons's first demodulation method is the "Asynchronous Half-Wave Envelope Detection". The first such receiver used a crystal to create a diode. This method led to one of the first, massed produced AM receivers. Those were "cat's whisker" receivers, a form of crystal receiver. These receivers started with an external antenna, a loop of wire that was used to tune the receiver, a nonlinear junction (the "cat's whisker" combined with a crystal) that acted as a diode, and a headphone output.

This first circuit is one of the first nonlinear demodulation methods. The crystal acts as a diode, which half-wave rectifies the modulated signal. The spectrum (below) shows a baseband signal (the original information), the original, modulated signal, plus copies of the signal at even harmonic frequencies.

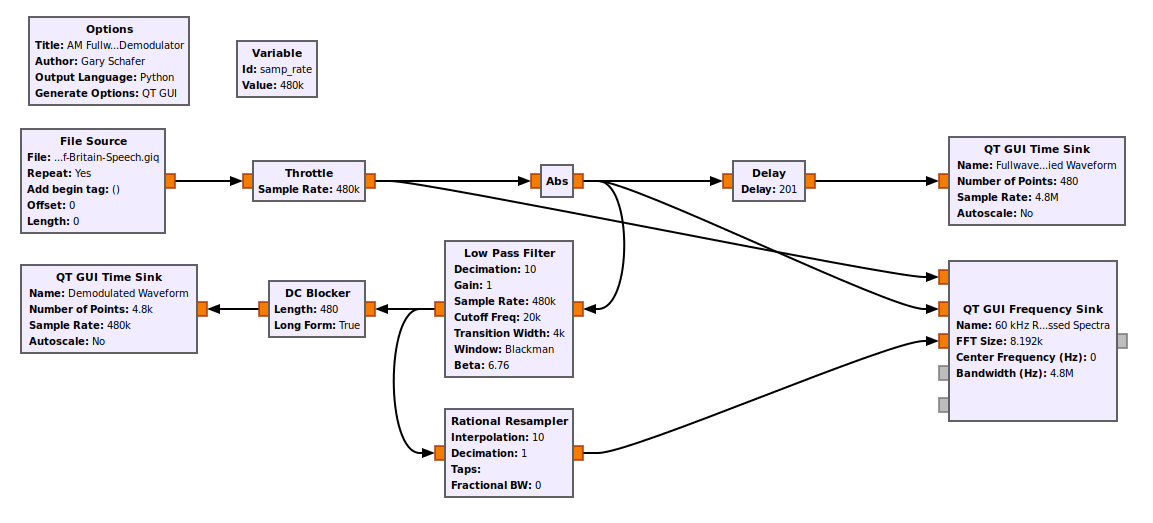
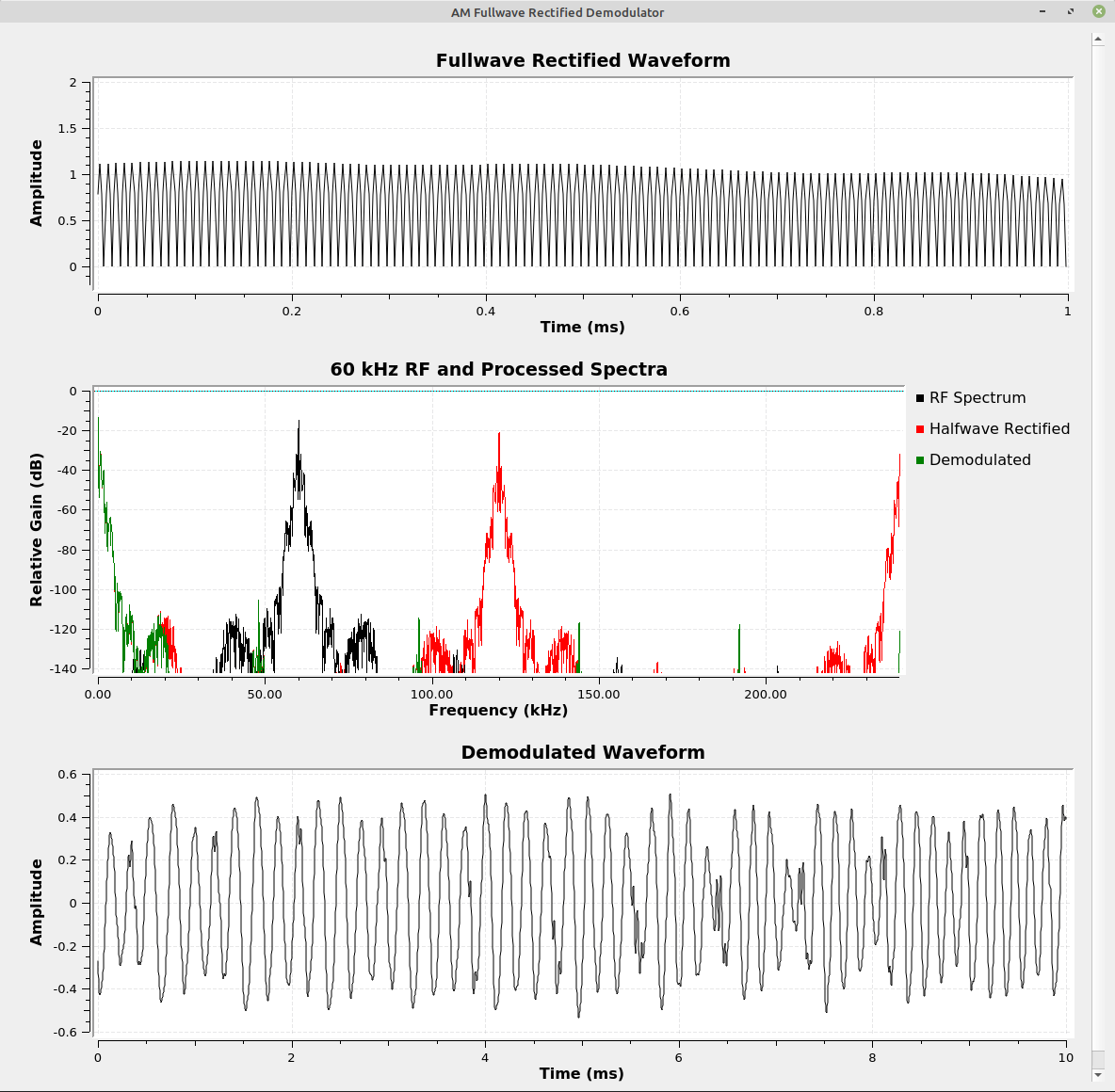
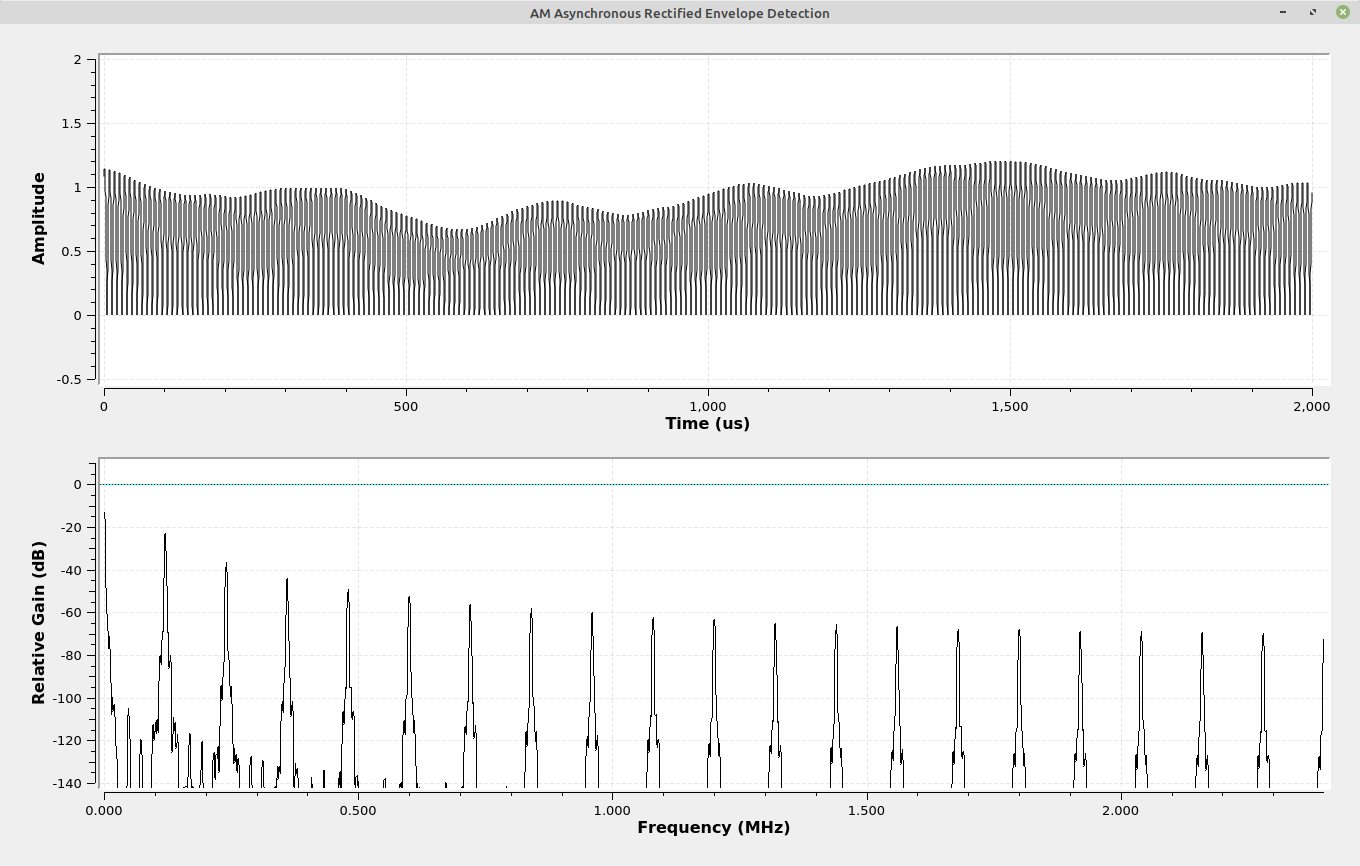
Full-wave Rectified Envelope Detection
A problem with the half-wave rectified receiver is that it essentially throws away half of the signal. To correct this, we can use a full-wave rectified circuit. It's typically a diode bridge consisting of four diodes. The diodes create a circuit in which the output will be a positive signal regardless of whether the input is positive or negative. In the digital domain, a full-wave rectified receiver can be created using the "Abs" function, as seen below. In an analog system, this would probably be a diode rectifier circuit in which two sets of diodes would provide for the full rectification of the modulated waveform.
Squared Rectified Envelope Detection
If you look at the spectrum of both the half-wave and full-wave rectified circuits, you'll see signals at the top end of the spectrum. Both the half-wave and full-wave circuits create harmonics that run off to... infinity.
This is not a problem for the original, analog circuits. It doesn't work so well in the digital realm. Such harmonics will create aliasing. This next circuit solves this problem. It uses the simple means of squaring the signal (multiplying it by itself). The result will be a baseband signal and a signal at twice the frequency. There will be no higher order harmonics than the second harmonic. Hence, no aliasing.
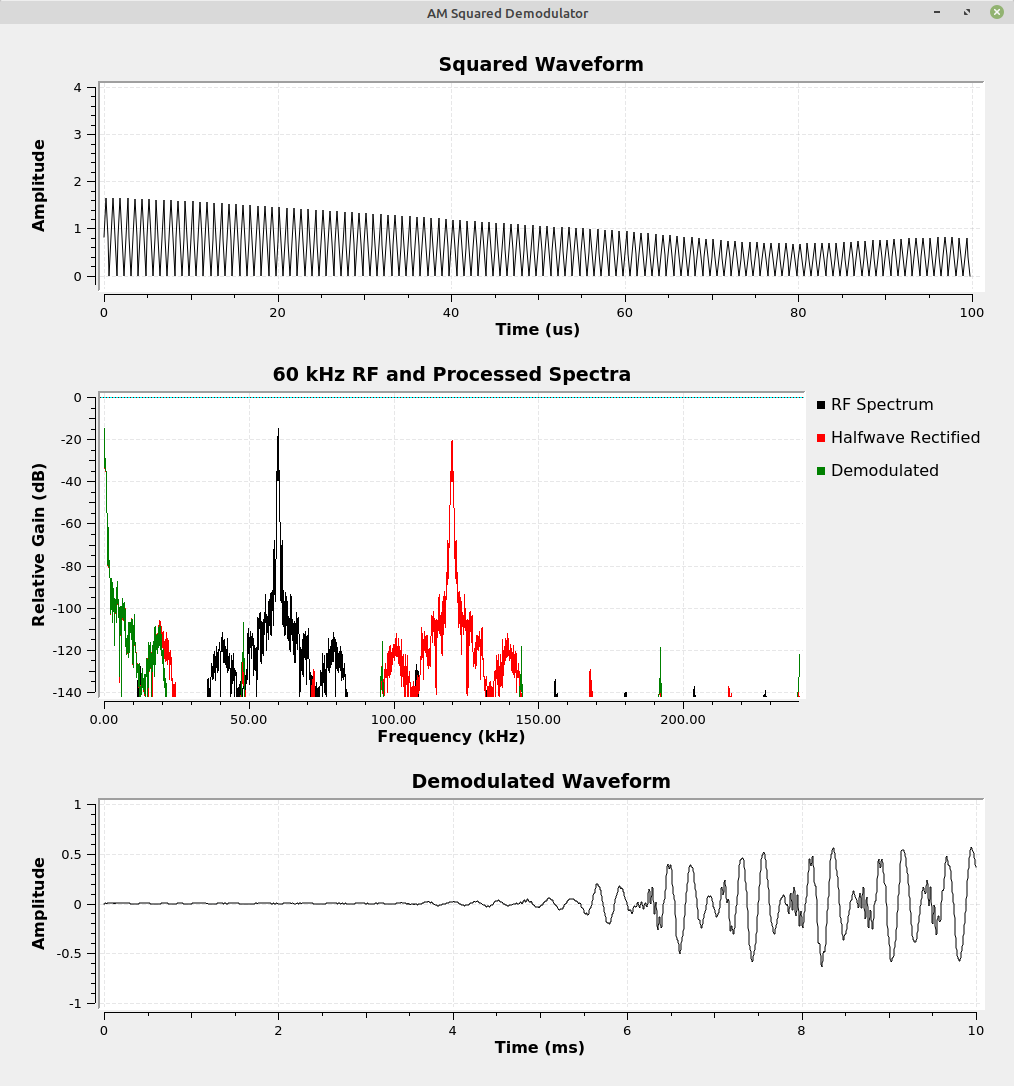
The only issue with this circuit is that the squaring operation requires a de-squaring (square rooting?) operation in order to bring the amplitude levels back to normal. For this operation, I used the "Transcendental" block to calculate the square root. Note that there's a "Rail" block just before the "Transcendental" block with the "sqrt" function. The reason for the "Rail" block is to prevent any values less than 0. The "sqrt" function cannot handle negative values. I discovered that, when the graph first starts running, there could be negative values that occur. The "Rail" block prevents that.
Envelope Detection with Complex Signals
Up til now, all of the signals and processing have used real, not complex, signals. Lyons's next, few circuits change that. While each circuit starts with a real signal, the signals are converted to complex. The complex conversion takes one of two forms:
- Hilbert Transform: The first method simply uses the Hilbert transform to convert the signal from real to complex. This keeps the signal at the same center frequency, but eliminates the negative frequency signal. The first "Asynchronous Complex Envelope Detection" and the "Asynchronous Complex Square-Law Envelope Detection" are of this type.
- Quadrature Demodulator: The second method is the traditional method to convert any signal from real to complex. It uses a pair of sinusoid oscillators, 90 degrees out of phase with each other, followed by a lowpass filter for each, to convert the signal into complex. The difference from the Hilbert transform is that, in this case, the signal will be frequency shifted by the frequency of the oscillators. The second "Asynchronous Complex Envelope Detection" is of this type.
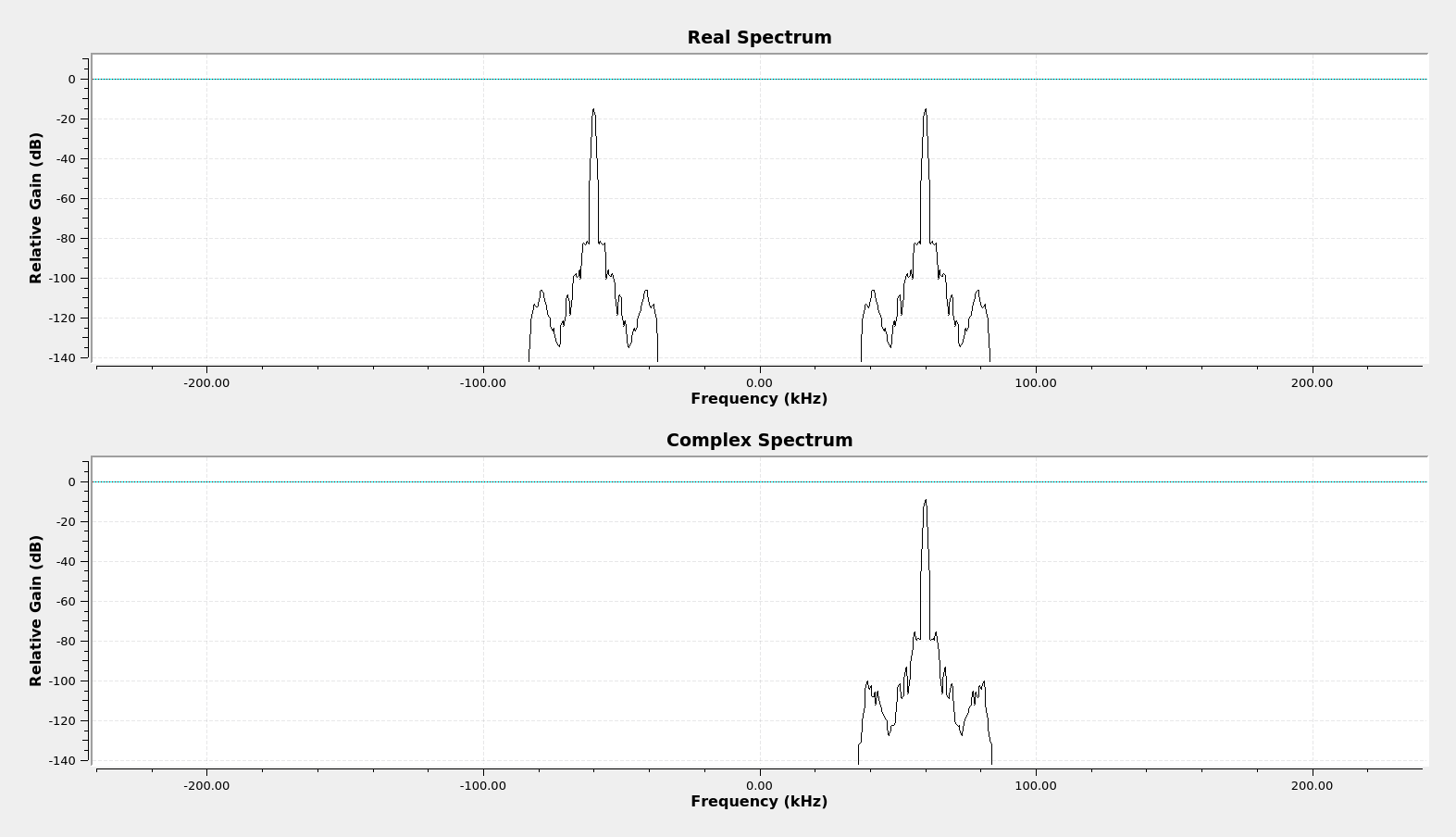
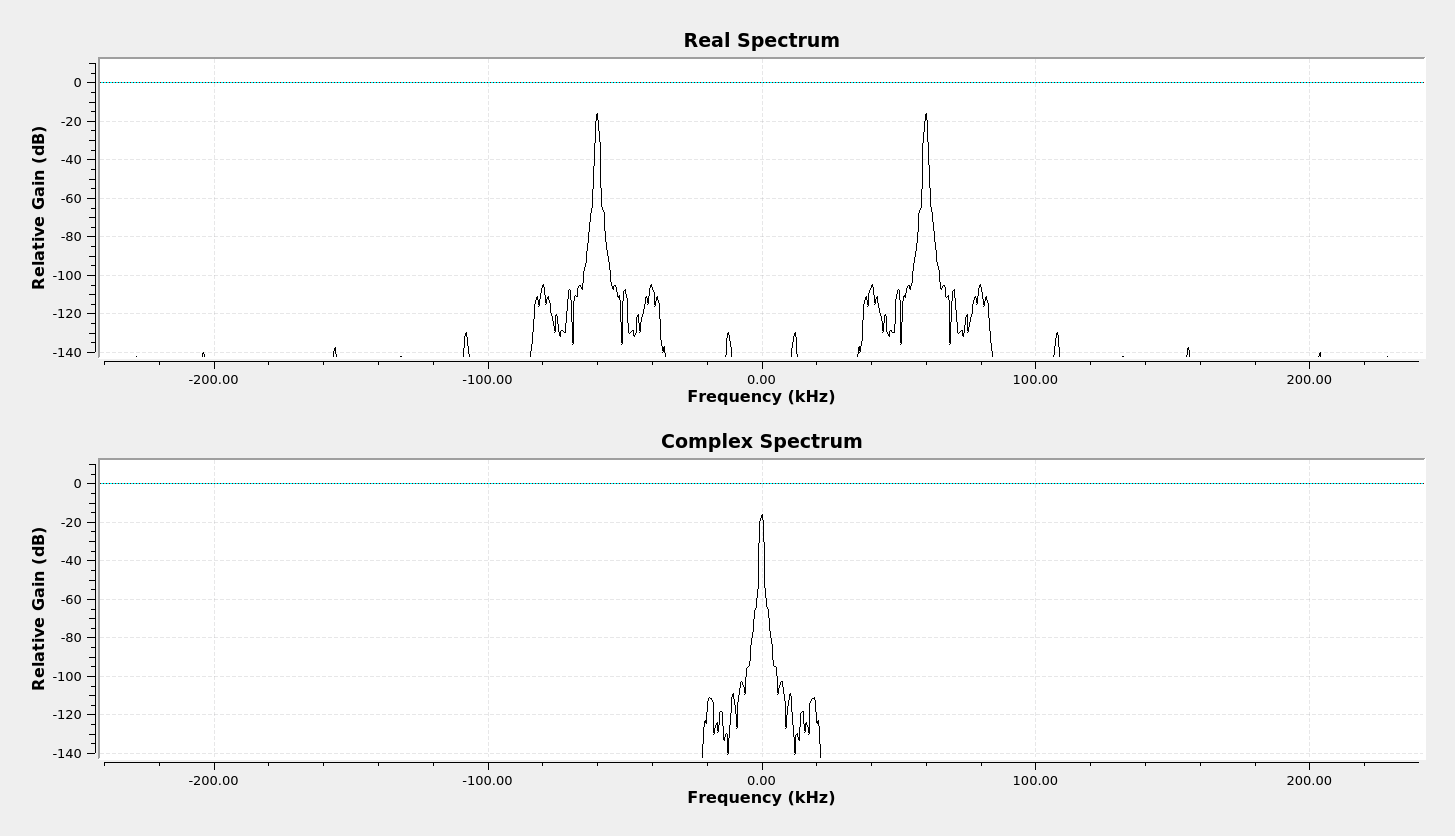
What I noticed looking at the block diagrams for the various asynchronous (noncoherent) envelope detection methods is that they're similar, if not the same, as those for the real signals. The difference is that you have to do each of them twice, one each for the real and imaginary component.
Asynchronous Complex Full-Wave Envelope Detection
This first complex system makes use of the Hilbert transform to translate the signal from a double-sided real signal into a single-sided complex signal. It takes each leg of the complex signal, both real and imaginary, and performs full-wave rectification on each.

This is where we see a difference between the real and complex operations. In the rectification of the real signal, the spectrum showed even numbered harmonics (2, 4, 6, etc). The spectrum of the complex rectified only shows every 4th harmonic (4, 8, 12, etc).

Asynchronous Complex Squared Envelope Detection
This graph is similar to the last one. The real signal is first passed through the Hilbert transform in order to create a complex signal. The real and imaginary components of the complex signal are squared individually, then the products added together. The result is a signal at baseband plus a signal at twice the original modulated frequency. The lowpass filter removes the signal at twice the frequency, leaving the information signal.

The graph above implements the magnitude squared function. It turns out that the "Complex to Mag" block will also work. Further, it provides the proper amplitudes.
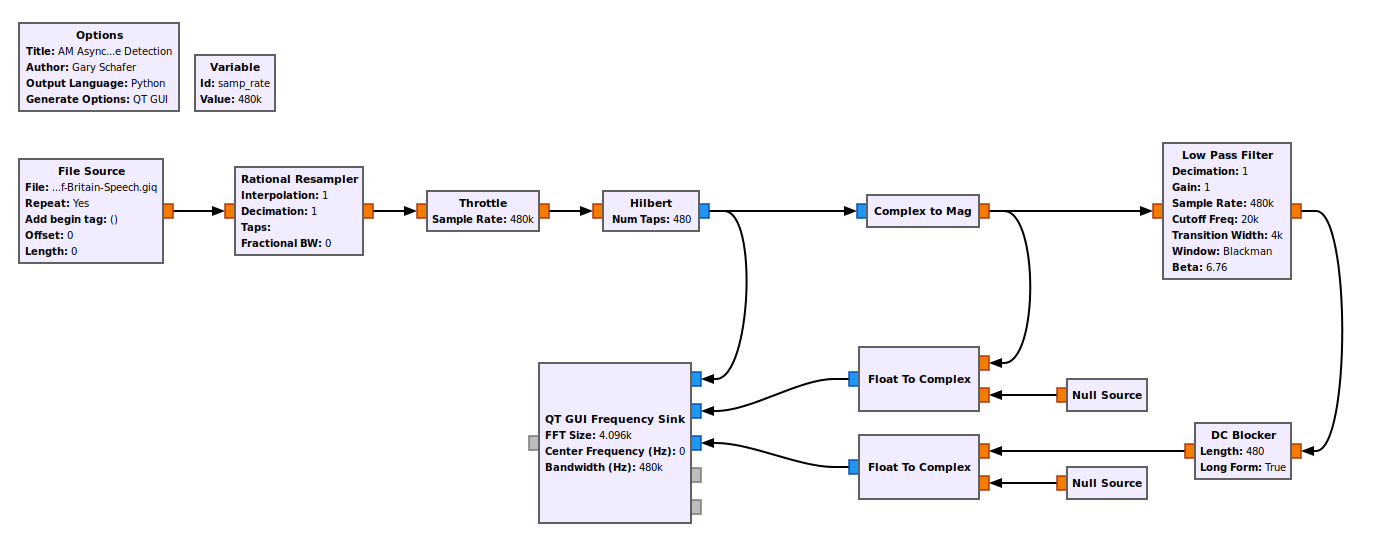
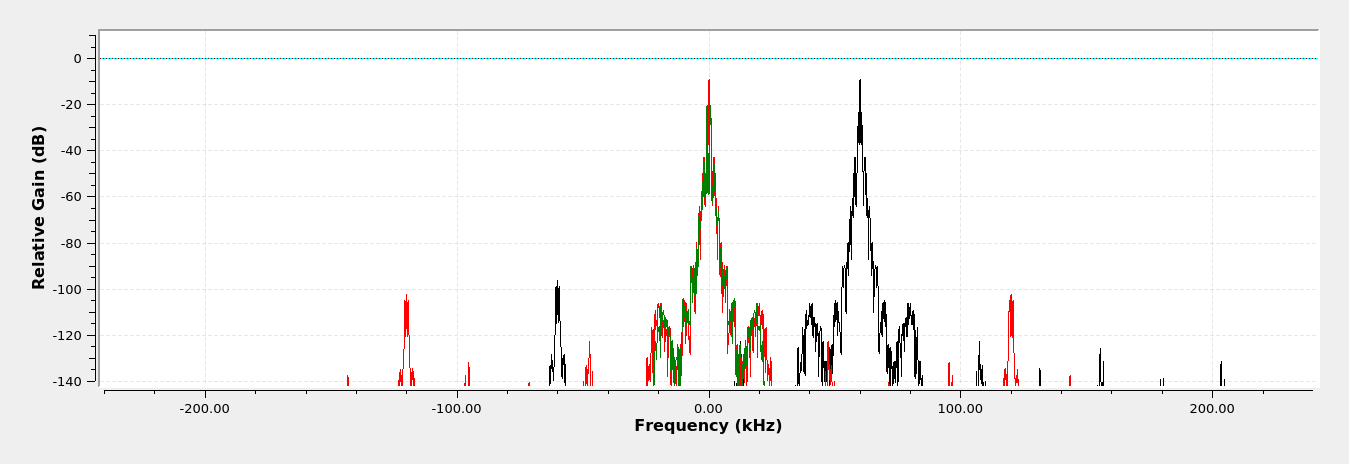
Asynchronous Quad Demod Complex Squared Envelope Detection
This last one is interesting. It turns the real signal into a complex signal using a quadrature demodulator. This consists of two sinewave generators that are in sync, but are 90 degrees out of phase. These sinewave signals are mixed with the modulated signal. After this, they're squared, added and lowpass filtered.
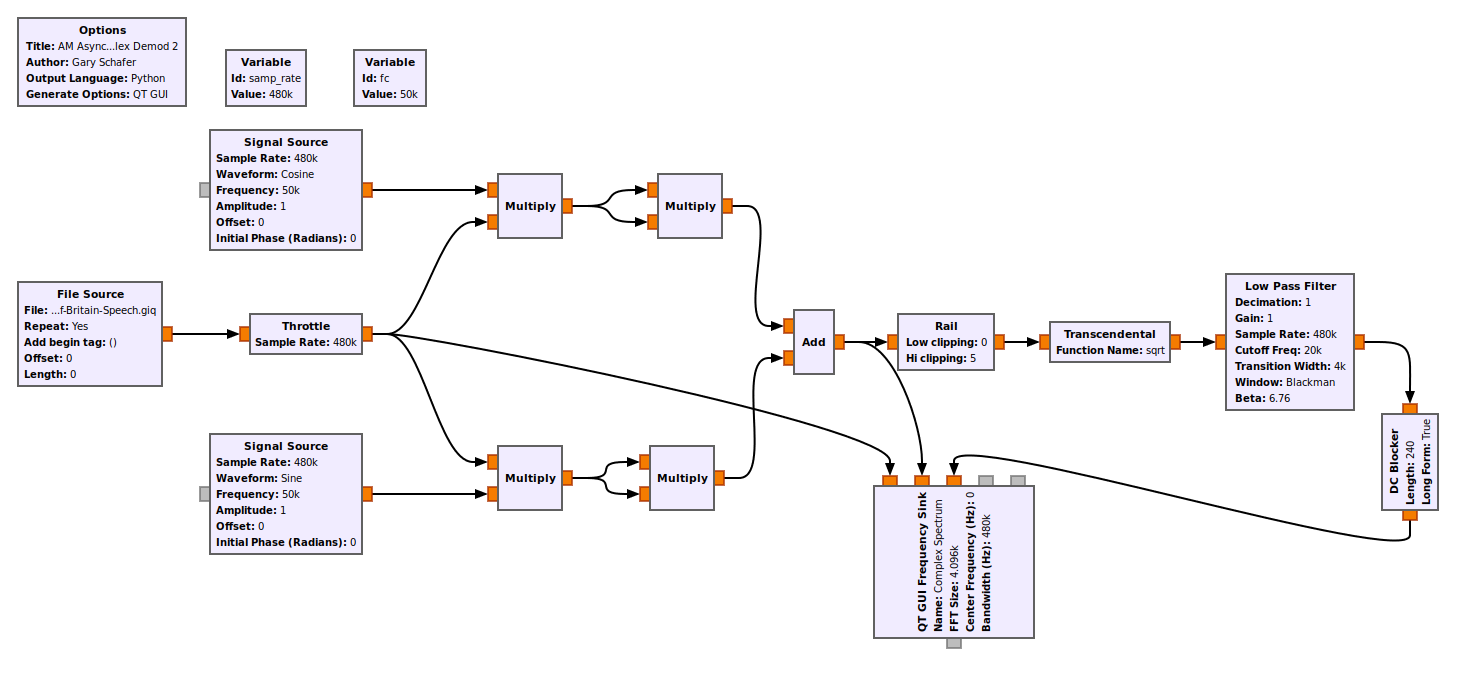
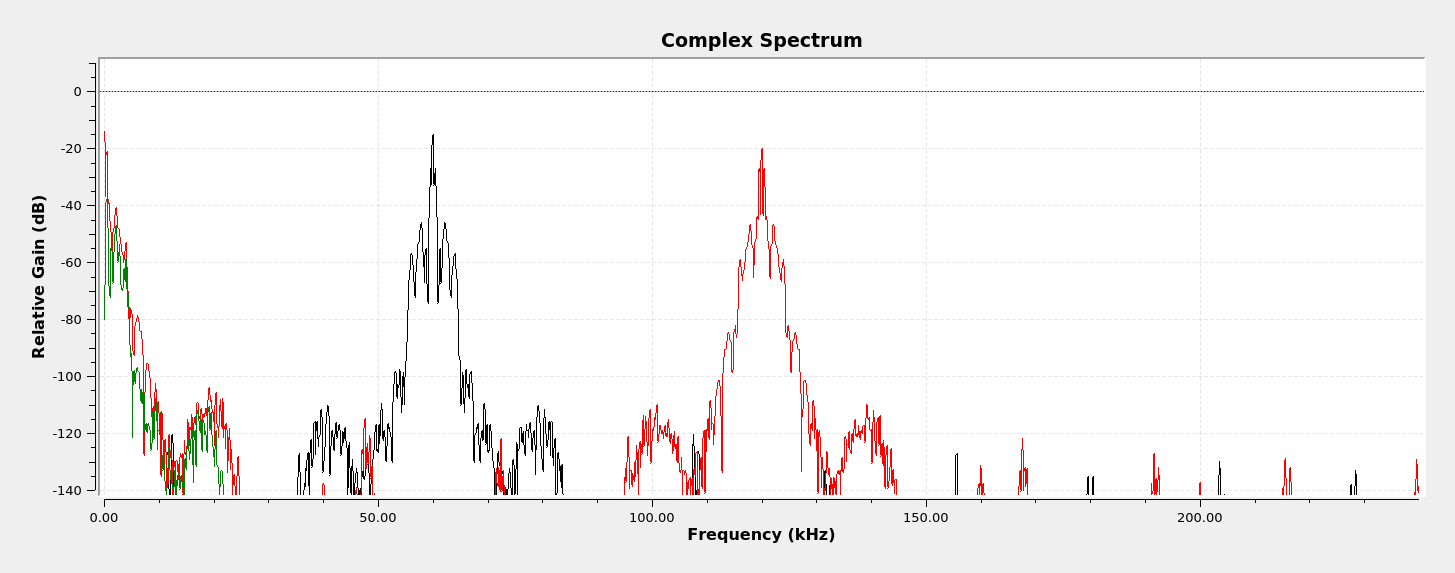
According to Lyons's article:
This detector is asynchronous in operation because the local oscillators' fo frequency need not be equal to the fc frequency of the incoming modulated RF signal. An fo within 25% of fc is acceptable so long as the lowpass filters sufficiently attenuate spectral energy near |fc+fo| Hz.
Because the I(n) and Q(n) sequences are in quadrature, phase cancellation occurs in the adder such that only spectral energy in the vicinity of zero Hz appears at the adder's output. As such, this detector is very tolerant of local oscillator frequency/phase drift just so long as the local cosine/sine oscillators remain in quadrature.
However, what I discovered while playing around with this circuit was that the frequency of the sinewaves did not matter. The output signals looked the same regardless, and the signal properly demodulated regardless of the sinewave frequencies. I shifted it in 1 kHz increments between 0 - 100 kHz. The output was the same for all of them.
Synchronous Real Envelope Detection
This last one is the one that must be used if the AM signal is using suppressed carrier. Further, for some signals (digital, for example), the sinusoid generator must be in phase sync with the modulated waveform. However, if the signal is full carrier, then it becomes easier to deal with. A full carrier AM signal can be demodulated without having to phase sync with the modulated signal.
In the case of Gnu Radio, the input is probably already a complex signal. For example, if you are using any of the common, inexpensive SDRs (RTL-SDR, HackRF, SDRPlay, LimeSDR), then a full carrier AM signal could be demodulated simply by ensuring that the signal is properly filtered, followed by using a "Complex to Mag" block to recover the information.
For the case of a suppressed carrier AM signal, it depends on how tolerant the signal is to a frequency / phase offset. (NOTE: A frequency offset would create a constant phase offset, since frequency is a change of phase over time.) Audio signals, for example, could easily tolerate a frequency offset of tens of Hz. But a digital signal would require some type of frequency and phase synce. A friend of mine, an amateur radio enthusiast, states that a double sideband signal can be synced using a basic Costas loop. A single sideband, though? That would require a more sophisticated demodulator.
Unfortunately, the Costas loop in Gnu Radio is not the type that can be used on analog signals. It's designed for digital signals. Hence, I'll leave actual tests of coherent circuits for a later post (if I do one at all). UPDATE: The Costas loop can be used to demodulate suppressed carrier AM signals. It requires that the signal be double sideband, but otherwise the Costas loop will work using an "Order" of 2. The loop bandwidth almost always works fine with a value of "2*math.pi/100".
Summary
This was an interesting post to create. When I first started it, I figured it would take a few days to put it together. I've been working on it now for six weeks. Once again, Dr. Lyons piqued my curiosity enough that I've spent the past six weeks trying out different graphs in Gnu Radio, mostly for the noncoherent circuits.
Given what I've learned, I'd expect the squared circuit to be the best. Why? Because the spectrum only shows a signal at twice the original frequency. The other noncoherent circuits also have many harmonics. I consider those other harmonics to be wasted energy. They do not add anything to the demodulated signal. They're simply filtered out. The main thing I learned was that they all work for basic audio signals. Regardless of the graph, they all demodulate full carrier audio signals with little to no distortion. In my mind, the result is that I would choose the one that is the simplest to create in Gnu Radio.